第1章 はじめに

1.1 統計的手法の目的

医療機器にとって最も重要な要件は、その意図する用途（Intended use）に基づき、適切な使用法において安全かつ有効に使用されることが保証されなければならないということである。このために、医療機器の開発から製造において、完成機器またはその構成要素であるユニットや部品などの要求事項を満足させることが保証できること、および医学的に安全で有効であることを確実にする必要がある。

こうした保証を得るため、臨床評価、設計開発の検証（ベリフィケーション）、設計開発の妥当性確認（バリデーション）、製造工程における検査などの活動が行われる。統計的手法は、これらの製品実現のための活動において、それらの結果が統計的に有意であると主張することにより、より確実な方向に導くことを支援することを目的としている。

1.2 ISO 13485における統計的手法の要求事項

ISO 13485では、以下の項目において統計的手法の使用が要求されている：

設計・開発の検証（7.3.6項）においては、設計・開発からのアウトプットが設計・開発へのインプットの要求事項を満たしていることを確実にするために、計画し文書化した取り決めに従って設計・開発の検証を実施することが求められる。組織は、方法および許容基準を含む検証計画を文書化する必要があり、これには該当する場合、サンプルサイズの根拠とした統計的手法を含めることが要求されている。

設計・開発のバリデーション（7.3.7項）では、結果として得られる製品が規定した適用または意図した使用への要求事項を満たす能力があることを確実にするために、計画し文書化した取り決めに従って実施することが求められる。組織は、方法および許容基準を含むバリデーション計画を文書化する必要があり、ここでも該当する場合にはサンプルサイズの根拠とした統計的手法を含めることが要求されている。

製造およびサービスの提供（7.5項）においては、プロセスのバリデーションの手順を文書化する際に、適切な場合にはサンプルサイズの根拠となる統計的手法を含めることが要求されている。

1.3 統計的手法の適用範囲

QMSのステップに応じて、統計的手法は様々な場面で活用することができる。製品設計開発段階では、大きさ、重さ、強さ、機能の決定、要求事項への適合性評価、ばらつきの管理などに検定と推定、実験計画などの手法が用いられる。

製造工程設計開発においては、製造・試験基準の決定や製造・試験バリデーションにおいて、稼働条件の最適化や要求事項への適合性評価に統計的手法が活用される。

製造段階では、製造管理や品質管理において、規格への品質適合の確認や工程管理に抜取検査、工程能力評価、管理図などの手法が使用される。

市販後管理においては、製品の監視測定や想定外のイベント監視にQC七つ道具や新QC七つ道具などのツールが活用される。

QMSのステップ	統計的手法が利用できる場面	統計的手法の例
製品設計開発 •製品仕様の検討 •設計検証 •設計バリデーション	•大きさ、重さ、強さ、機能の決定 •要求事項への適合性評価 •ばらつきの管理	•検定と推定 •実験計画
製造工程設計開発 •製造・試験基準の決定 •製造・試験バリデーション	•稼働条件の最適化 •要求事項への適合性評価 •
製造 •製造管理 •品質管理	•規格への品質適合の確認 •工程管理	•抜取検査 •工程能力 •管理図
市販後管理 •製品の監視測定	•想定外のイベント監視	•QC七つ道具 •新QC七つ道具

1.4 製品要求事項の保証

製品実現の活動において、製品要求事項が保証されることが確実にされていなければならない。このために検証やバリデーションなどにおいて、統計的手法による有効性を主張することを考慮する必要がある。

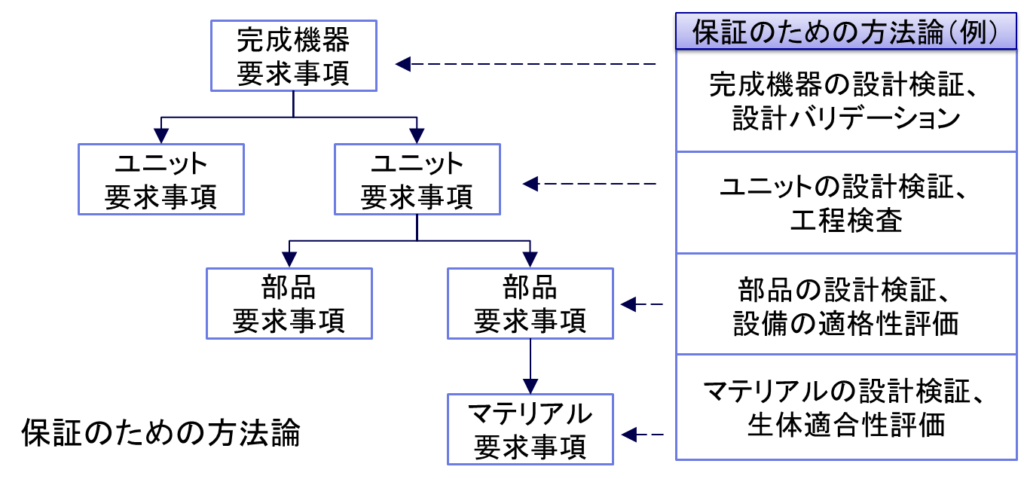
完成機器、ユニット、部品、マテリアルという各階層において、それぞれの要求事項に対する保証方法を確立する必要がある。完成機器に対しては設計検証および設計バリデーション、ユニットに対してはユニットの設計検証や工程検査、部品に対しては部品の設計検証や設備の適格性評価、マテリアルに対してはマテリアルの設計検証や生体適合性評価などが実施される。これらの活動において統計的手法を適切に活用することが重要である。

1.5 統計手法の基本的な分類

統計的手法は大きく記述統計と推測統計の二つに分類される。記述統計は、あるデータを集めて表やグラフを作り、平均や傾向を見ることでデータの特徴を把握するものである。工程の状態の把握、苦情率や不適合率の推移の把握、苦情原因等の把握などに用いられる。

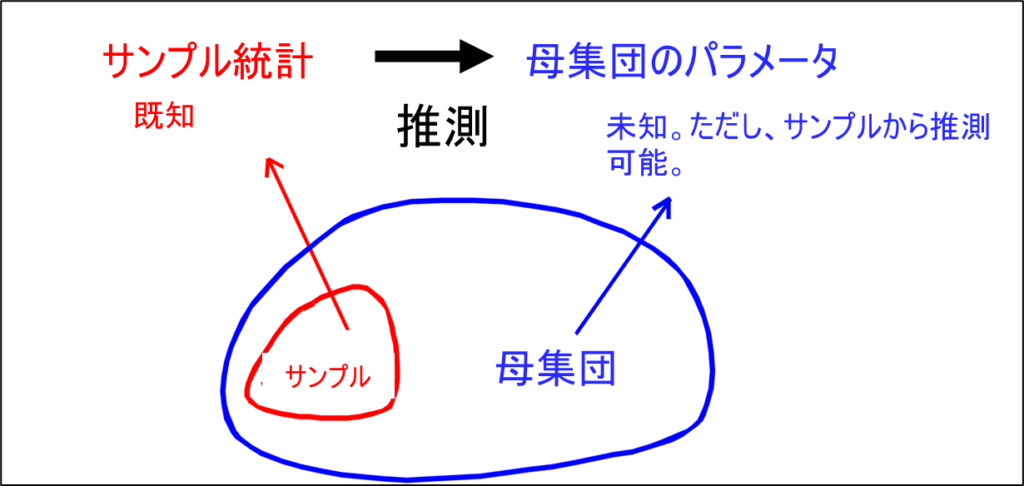
一方、推測統計は、母集団からサンプルを抜き取って、そのサンプルの特性から母集団の特性を推測し、それが正しいかどうかを検定する手法である。製造における抜き取り検査やサンプリングを伴う設計検証、妥当性確認等に用いられる。

1.6 サンプルサイズに関する重要な考え方

サンプルサイズに関して、「サンプルサイズは大きい方が良い」という考え方や、「手間を考えてなるべくサンプルサイズを小さくしたい」という考え方がよく見られる。しかし、これらはいずれも誤りである。サンプルサイズは「何人以上」ではなく、「何人」という具体的な数値として決定されなければならない。

サンプル数（the number of samples）とサンプルサイズ（sample size）は異なる概念である。サンプル数は何回標本抽出を行ったか（群数、標本数）を表し、サンプルサイズは1回の標本抽出において何個体を調べたか（各標本、各群の個体数、N数）を表す。

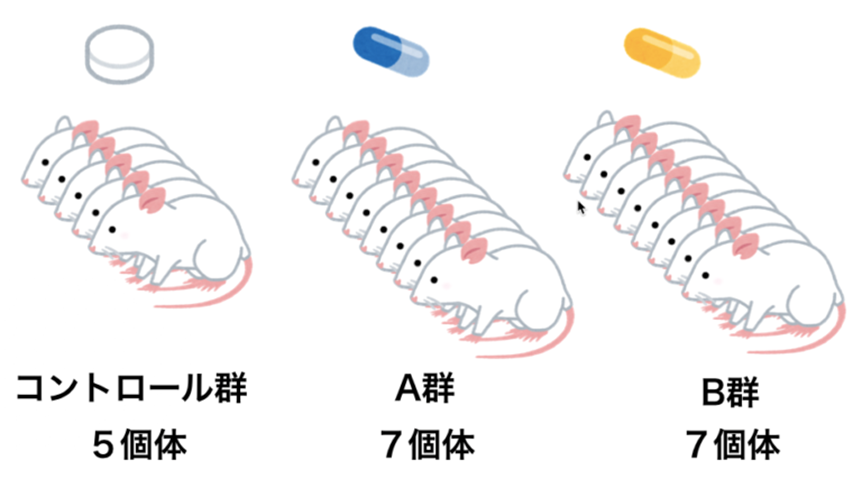
例えば、がんを発症したマウスに対して、コントロール薬、A薬、B薬（それぞれC群、A群、B群とする）を投薬し、一定時間経過後、腫瘍径の母平均の差を比較する実験を行う場合、C群、A群、B群それぞれに対して5、7、7個体のデータを取得したとすると、サンプル数（群数）は3、サンプルサイズ（各群のサイズ）はC群が5、A群が7、B群が7となる。

1.7 統計的手法の重要なポイント

統計的手法を適用する際の重要なポイントとして、まず母集団全体を把握できない場合にサンプリングが必要となることを理解しなければならない。全数把握が可能な場合（例えば最終検査や苦情管理など）と異なり、購入したネジ100万本の受入検査やある工作機械で製造する製品のばらつきを評価する場合などでは、サンプリングが不可欠となる。

ただし、ばらつきのないものに関しては、N=1で十分な場合もある。例えば、よく混ぜた味噌汁のように、どこを測定しても同じ特性を示すものがこれに該当する。このような場合、一昼夜放置して上澄み、真ん中、鍋底で味が異なってくるような状況とは違い、十分に撹拌された状態では一つのサンプルで代表値として扱うことが可能である。

サンプリングは本質的に確率論に基づくものであり、この特性を十分に理解する必要がある。サンプルサイズが小さいと有意差が出にくく、大きいと有意差が出やすい（P値が小さくなる）という特徴がある。また、群間の差（効果量）が大きいと有意差が出やすい（P値が小さくなる）という性質も持っている。

1.8 サンプルサイズ決定の基本原則

サンプルサイズを決定する際には、以下の四つの要素を考慮する必要がある：

群間の効果の差（効果量）、ばらつき（サンプルの標準偏差）、有意水準（P値、信頼度、αエラーを防ぐ力）、そして検出力（検定力、パワー、βエラーを防ぐ力）である。これら四つの要素が決まれば、サンプルサイズは自動的に決定される。

一般的な基準値として、有意水準αは0.05（5%）、検出力（1-β）は80%を用いることが多い。これらの値を用いて、統計ソフトウェアまたはExcelを使用してサンプルサイズを計算することができる。計算式を暗記する必要はなく、適切なソフトウェアツールを活用することが推奨される。

1.9 まとめ

本章では、医療機器における統計的手法の重要性と、特にサンプルサイズ決定の基本的な考え方について説明した。統計的手法は、製品の安全性と有効性を確保するための重要なツールであり、ISO 13485の要求事項としても明確に規定されている。

サンプルサイズの決定は、単純に「大きければ良い」あるいは「小さければ良い」というものではなく、科学的な根拠に基づいて適切な数を決定する必要がある。これは効果量、ばらつき、有意水準、検出力という四つの要素を考慮することで達成される。

次章からは、これらの概念をより詳細に説明し、実際の適用方法について具体的に解説していく。