第11章 例題
11.1 例題1:一つの母平均の検定におけるサンプルサイズの検討(母分散既知)
バッテリー充電時間の母平均が40分、母標準偏差が2分の場合において、充電時間の平均が2分以上変わったかを検定したい状況を考える。この場合、α=5%、β=10%として検討を行う。
まず、一つの母平均の差(分散既知)について考え、対立仮説はμ≠μ₀と設定する。サンプルサイズの近似値は以下の式で求められる。
n=(zα/2-z1-β/Δ₀)² = (z0.025-z-0.1)/(2/2))² = (1.960-(-1.282)/1)² ≒ 10.51
次に検出力の確認として、n=10の場合とn=11の場合の検出力を計算する。
n=10の場合:
1-β = Pr(u≦-Zα/2-√nΔ) + Pr(u≧Zα/2-√nΔ)
= Pr(u≦-1.960-√102/2) + Pr(u≧1.960-√102/2)
= Pr(u≦-5.122) + Pr(u≧-1.202)
= -0.000 + 0.885 = 0.885
n=11の場合:
1-β = Pr(u≦-Zα/2-√nΔ) + Pr(u≧Zα/2-√nΔ)
= Pr(u≦-1.960-√112/2) + Pr(u≧1.960-√112/2)
= Pr(u≦-5.277) + Pr(u≧-1.357)
= -0.000 + 0.913 = 0.913
これらの計算結果から、1-β≧90%となるサンプルサイズは11であることが判明した。
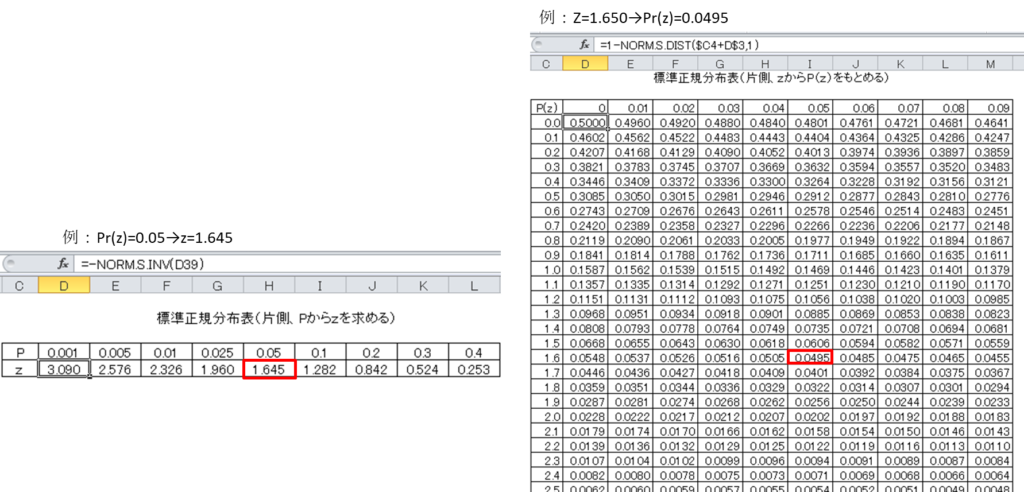
11.2 正規分布表
正規分布表は、検定における確率計算に必要不可欠な参照データである。以下に例を示す:
- Z=1.650 → Pr(z)=0.0495のように、Z値から確率を求めることができる
- Pr(z)=0.05 → z=1.645のように、確率からZ値を求めることができる
正規分布表では、P=Pr(z)として以下のような対応関係を示している:
11.3 例題2:一つの母平均の区間推定に対するサンプルサイズの検討(母分散既知)
バッテリー充電時間の母平均が40分、母標準偏差が2分の場合において、充電時間の平均を95%信頼区間の区間幅で3分以下になるようにしたい状況を考える。
サンプルサイズの計算は以下の式で行う。
n ≧ (4Z²α/2*σ₀²)/Δ²
この式に値を代入すると:
41.960²2²/3² = 61.4656/9 = 6.83
したがって、サンプルサイズは7以上とする必要がある。
11.4 例題3:一つの母平均の検定におけるサンプルサイズの検討(母分散未知)
バッテリー充電時間の母平均が40分、母標準偏差が未知の場合において、充電時間の平均がΔ((μ-μ₀)/σ)=0.5以上短くなっているかを検定したい状況を考える。この場合、α=5%、β=5%として検討を行う。
一つの母平均の差(分散未知)について、対立仮説はμ>μ₀と設定する。サンプルサイズの近似値は以下の式で求められる。
n ≒ ((zα-z1-β)/Δ₀)² + z²α/2/2
= ((z0.05-z0.95)/0.5)² + z²0.05/2
= ((1.645-(-1.645))/0.5)² + 1.645²/2
= 44.65
検出力の確認として、n=44の場合を計算する:
1-β ≒ Pr(t₀≧t(φ,2α))
= 1 – Pr[u≦(t(43,0.1)(1-1/(443))-√440.5)/√(1+t(43,0.1)²/2*43)]
= 1 – Pr[u≦-1.620]
= 0.947
同様にn=45の場合を計算すると、1-β=0.951となる。
これらの計算結果から、1-β≧95%となるサンプルサイズはn=45であることが判明した。
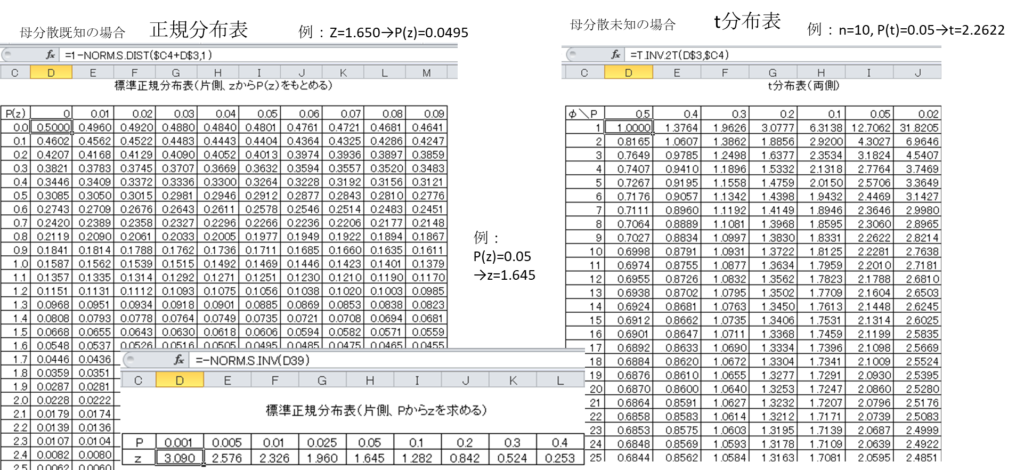
11.5 正規分布表とt分布表
統計的検定において、母分散が既知の場合は正規分布表を、母分散が未知の場合はt分布表を使用する。
正規分布表(母分散既知の場合)
正規分布表では以下のような対応関係を参照できる:
- Z=1.650 → P(z)=0.0495
- P(z)=0.05 → z=1.645
t分布表(母分散未知の場合)
t分布表の使用例:
- n=10、P(t)=0.05の場合 → t=2.2622
11.6 例題4:一つの母平均の区間推定におけるサンプルサイズの検討(母分散未知)
バッテリー充電時間の母平均が40分、母標準偏差が未知の場合において、充電時間の平均の信頼区間がΔ3分以下になるようにサンプルサイズを決定したい状況を考える。予備実験より標準偏差は2分と推定できており、信頼率は1-β=95%とする。
まず、サンプルの標準偏差を計算する(予備実験より)σ=2.0とする。次に、標準偏差既知と仮定し、母平均の区間推定に対するサンプルサイズを計算する。例題2よりn=7が得られる。
区間推定のサンプルサイズの式に、得られたサンプルサイズ以上の数を順次当てはめ、Δ3.0以下になるサンプルサイズを計算する。
n=7の場合:
2t(n-1,α)cσ/√n = 22.44690.95942/2.646 = 3.55
n=8の場合:
2t(n-1,α)cσ/√n = 22.36460.96502/2.828 = 3.23
n=9の場合:
2t(n-1,α)cσ/√n = 22.30600.96932/3 = 2.98
これらの計算結果から、n=9の時にΔ3.0以下になるため、サンプルサイズは9と決定される。
11.7 C表
| φ | c | φ | c |
|---|---|---|---|
| 1 | 0.7979 | 25 | 0.9901 |
| 2 | 0.8862 | 30 | 0.9917 |
| 3 | 0.9213 | 35 | 0.9929 |
| 4 | 0.9400 | 40 | 0.9938 |
| 5 | 0.9515 | 45 | 0.9945 |
| 6 | 0.9594 | 50 | 0.9950 |
| 7 | 0.9650 | 55 | 0.9955 |
| 8 | 0.9693 | 60 | 0.9958 |
| 9 | 0.9727 | 65 | 0.9962 |
| 10 | 0.9754 | 70 | 0.9964 |
| 11 | 0.9776 | 75 | 0.9967 |
| 12 | 0.9794 | 80 | 0.9969 |
| 13 | 0.9810 | 85 | 0.9971 |
| 14 | 0.9823 | 90 | 0.9972 |
| 15 | 0.9835 | 95 | 0.9974 |
| 16 | 0.9845 | 100 | 0.9975 |
| 17 | 0.9854 | ||
| 18 | 0.9862 | ||
| 19 | 0.9869 | ||
| 20 | 0.9876 |
C値は以下の計算式で求めることができる:
分子式:
- C値を計算するための分子部分の式
- =SQRT(2)*EXP(GAMMALN((φ+1)/2))
分母式:
- C値を計算するための分母部分の式
- =SQRT(φ)*EXP(GAMMALN(φ/2))
11.8 製品・プロセスのリスク評価における統計的手法の適用
製品とプロセスのリスク評価においては、統計的手法が必要となる製品(部品、ユニットを含む)、プロセスの持つリスクレベルを特定するための評価方法を確立する必要がある。この評価方法は各組織で自由に設定することが可能であるが、合理的な根拠に基づいて設定されなければならない。
リスク評価の結果に基づいて、サンプルサイズを決定するための基準となる設定表を作成することで、より明確な運用が可能となる。ただし、リスクに対してなぜそのレベルでよいのか、合理的な理由を文書化して残すことが必須である。
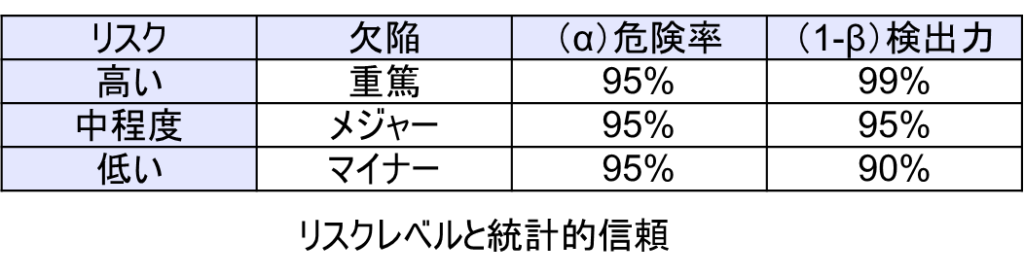
米国医療機器業界では、仮説検定において一般的に以下のような信頼度設定が使用されている:
リスクが高く、重篤な欠陥の場合:
- 危険率(α):95%
- 検出力(1-β):99%
リスクが中程度で、メジャーな欠陥の場合:
- 危険率(α):95%
- 検出力(1-β):95%
リスクが低く、マイナーな欠陥の場合:
- 危険率(α):95%
- 検出力(1-β):90%
ここで、危険率は信頼度(Confidence)とも呼ばれ、検出力は信頼性(Reliability)とも呼ばれている。
11.9 計数値(Attribute)試験におけるサンプルサイズ計算
計数値試験における信頼度(C)と信頼性(R)に基づくサンプルサイズの計算においては、特に試験の失敗を許容しない条件(失敗0)におけるサンプルサイズの決定が重要な課題となる。二項分布を想定した場合、以下の式でこの計算を実行できる:
n = ln(1-C)/ln(R)
ここで:
- n:サンプルサイズ
- C:信頼度
- R:信頼性
- ln:自然対数(ln x ≒ 2.303 log₁₀ x)
この式を用いて具体的な計算例を示す:
- 信頼度95%、信頼性99%で試験の失敗0を条件とした場合:
計算結果は298.7となり、サンプルサイズはn = 299と決定される - 信頼度95%、信頼性95%の場合:
計算結果からn = 59となる - 信頼度90%でサンプルサイズn = 32の場合の信頼性計算:
R = (1-C)^(1/(n+1))
R = (1-0.90)^(1/(32+1))
R = 93.26%となる
この二項分布に基づく計算方法の大きな利点は、ロットサイズに依存せずに試験のサンプルサイズを設定できることにある。
11.10 計量値(Variable)試験におけるサンプルサイズ計算
計量値試験においては、信頼区間の推定や仮説検定といった統計的手法を適用する。サンプルの確率分布を想定することで、適切なサンプルサイズを計算することが可能となる。
11.10.1 平均値の信頼区間(分散既知の場合)
母集団の標準偏差σが既知で、サンプルサイズnの場合、母集団平均μに関する両側100%(1-α)信頼区間は以下の式で表される:
P(x̄ – δ < μ < x̄ + δ) = 1 – α
ここで、δ = (Z_α/2 * σ) / √n である。
指定された誤差δ(通常は0.5σから1.5σの範囲で設定される)における信頼区間を得るために必要なサンプルサイズは以下の式で計算できる:
n ≥ (Z_α/2 * σ / δ)^2
11.10.2 仮説検定
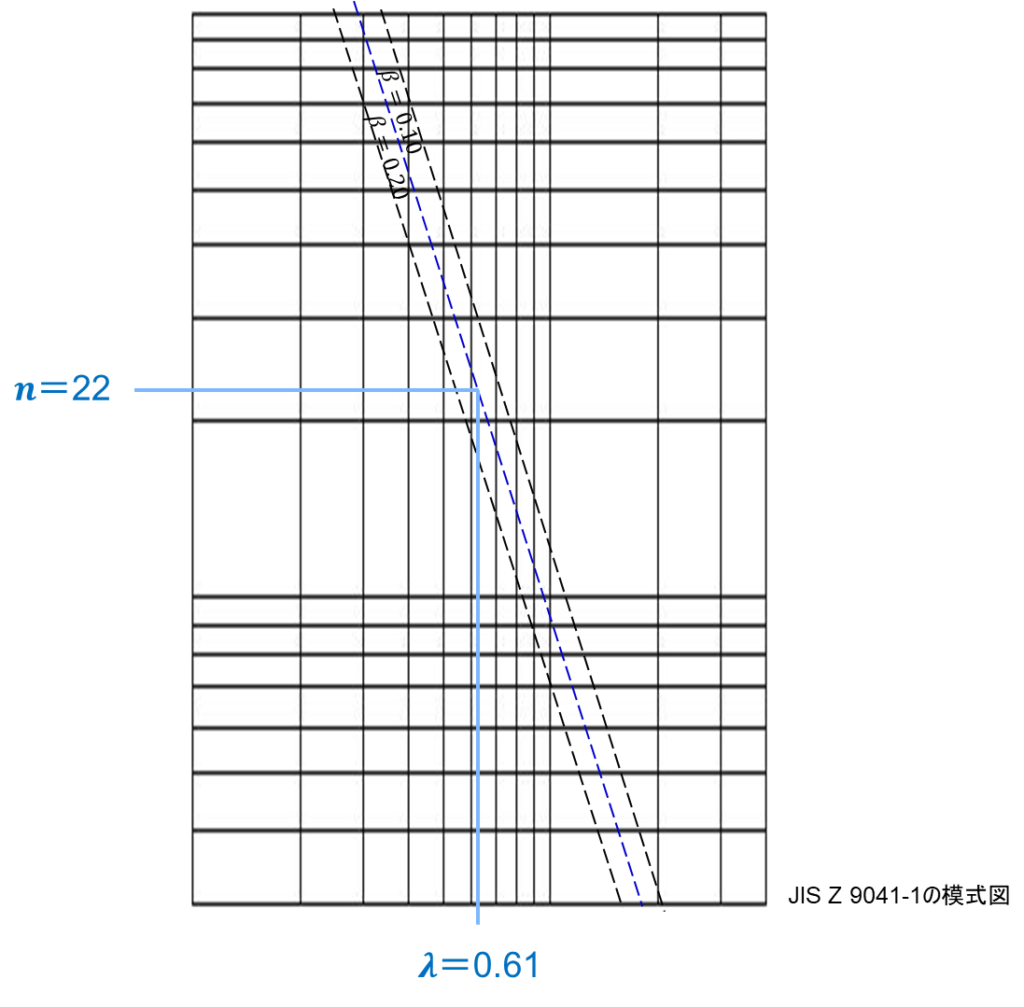
仮説検定の方法は、JIS Z 9041-2:1999「データの統計的な解釈方法―第2部:平均と分散に関する検定方法と推定方法」に規定されている。さらに、サンプルサイズを導く方法については、JIS Z 9041-4:1999「データの統計的な解釈方法―第4部:平均と分散に関する検定方法の検出力」に詳細が記載されている。
具体例として、綿糸の平均破壊負荷(単位:N)の保証について考える:
- 標準偏差σ = 0.33(既知)
- 平均の片側検定で仮説μ ≥ 2.30が棄却されない場合のみロットを受入
- μ = 2.10のときα = 0.05、β = 0.10
- パラメータλ = 0.61
この条件で JIS Z 9041-4の図3.2から読み取ると、必要なサンプルサイズはn = 22となる。
パラメータλの計算:
λ = (μ – μ_0) / σ = (2.30 – 2.10) / 0.33 = 0.61
11.10.3 平均の仮説検定(分散既知の場合)
帰無仮説H_0: μ = μ_0に対する対立仮説H_A: μ ≠ μ_0において、以下の条件で検定を行う:
- 標準偏差σは既知
- サンプル平均x̄はサイズnのサンプルから決定
- H_0における平均はμ_0
- 対立仮説H_Aの平均はμ_1 = μ_0 + δ
この場合、H_0を棄却するかどうかを決定する統計量は以下の式で与えられる:
z = (x̄ – μ_0) / (σ/√n)
H_0が棄却されない区間は:
P(-z_α/2 < z < z_α/2) = 1 – α
サンプルサイズnと検出力π = 1 – βで検出できる効果量(effect size)は:
δ = μ1 – μ_0 = (zα/2 + z_β) * σ / √n
真の平均がμ1 = μ_0 + δである場合にH_0を棄却する検定力は: π = P(-∞ < z < zβ)
ここで、z_β = (δ / (σ/√n)) – z_α/2
効果量δの特定の値に対して検出力π = 1 – βを得るために必要なサンプルサイズは:
n = ((z_α/2 + z_β)^2 * σ^2) / δ^2
具体例として、以下の条件で計算を行う:
- 母集団の標準偏差σ = 3.0(既知)
- H_0: μ = 30に対するH_A: μ ≠ 30の検定
- 90%の検出力でμ = 32へのシフト(差 = 2.0)を検出
計算:
δ = 2.0、Z_0.025 = 1.96、Z_0.10 = 1.28として
n = ((1.96 + 1.28)^2 * 3.0^2) / 2.0^2 = 24
実践的な例として、ロープの強度試験を考える:
ロープのサプライヤーが新製品の平均強度が10.0 kgを超えると主張している場合:
- 16本の試験片から得られた測定値:
9.9, 10.5, 11.0, 9.9, 10.4, 9.5, 9.6, 10.8, 9.8, 10.2, 11.3, 9.6, 10.3, 10.9, 10.6, 9.7 - 平均値:10.26 kg
- 標準偏差:0.55(既知)
- 帰無仮説:μ = 10
- 対立仮説:μ > 10
- 有意水準:α = 0.01
検定統計量の計算:
z = (x̄ – μ_0) / (σ/√n) = (x̄ – 10.0) / (σ/√16)
臨界値:Z_crt = Z_α = Z_0.01 = 2.326
(2.326より大きいZ_obsの値すべてがH_0の棄却域となる)
観測値の計算:
Z_obs = (10.26 – 10.0) / (0.55/√16) = 1.92
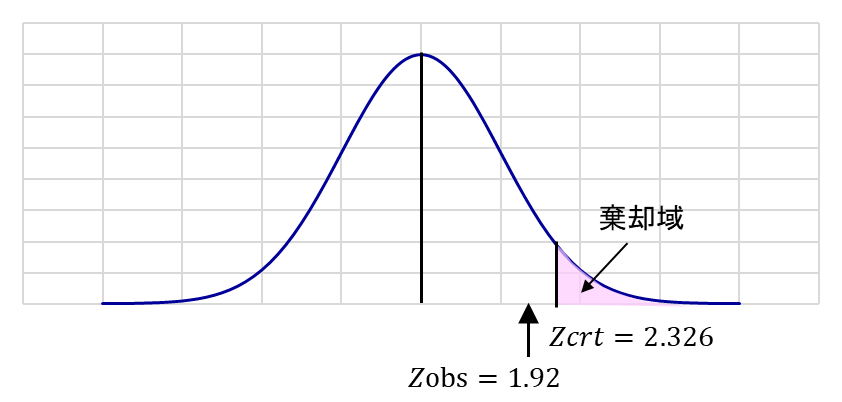
結果の解釈:
Z_obsは棄却域に存在しないため、H_0は棄却されない。したがって、ロープの母集団の平均強度は10 kg以下である可能性が否定できず、サプライヤーの主張は統計的に支持されない。
これは典型的な「片側検定」の例である。なお、H_1: μ > μ_0およびμ < μ_0のような対立仮説に対しては両側検定が必要となる。
11.10.4 平均の仮説検定(分散未知の場合)
標準偏差σが未知の場合の検定条件:
- 帰無仮説:H_0: μ = μ_0
- 対立仮説:H_A: μ ≠ μ_0
- サンプル平均x̄および標準偏差Sはサイズnのサンプルから決定
H_0を棄却するかどうかの統計量:
t = (x̄ – μ_0) / (S/√n)
H_0が棄却されない区間:
P(-t_α/2 < t < t_α/2) = 1 – α
(t分布の自由度:df = n – 1)
真の平均がμ = μ0 + δにシフトした場合にH_0を棄却する近似検出力: π = P(-∞ < t < tβ)
ここで、t_β = (δ/(σ̂/√n)) – t_α/2
検定力π = 1 – βを得るために必要なサンプルサイズの条件:
n ≥ ((t_α/2 + t_β)^2 * σ̂^2) / δ^2
具体例として以下の条件で計算を行う:
- H_0: μ = 30に対するH_A: μ ≠ 30の検定
- 危険率:5%
- 検出力:90%
- μ = 31へのシフトを検出
- 母集団の標準偏差は未知だが、σ ≈ 1.5と予想
- δ = 1.0
サンプルサイズの条件は自由度に依存するため、反復計算が必要となる:
第1回推測:
t ≈ z、Z_0.025 = 1.96、Z_0.10 = 1.28として
n = ((1.96 + 1.28)^2 * 1.5^2) / 1.0^2 = 23.62
第2回推測:
自由度df = 23、t_0.025,23 = 2.069、t_0.10,23 = 1.319として
n ≥ ((2.069 + 1.319)^2 * 1.5^2) / 1.0^2 = 25.83
第3回推測:
自由度df = 25、t_0.025,25 = 2.060、t_0.10,25 = 1.316として
n ≥ ((2.060 + 1.316)^2 * 1.5^2) / 1.0^2 = 25.49
この結果から、n = 26が妥当なサンプルサイズとして決定される。
11.11 プロセスバリデーションへの統計的手法の適用
プロセスバリデーションにおいては、何を統計的に評価するのかを明確にし、目的や条件に応じて適切な統計的手法を選択しなければならない。設計検証に適用できる統計的手法として、以下のようなものがある。
仮説検定を使用して製品要求事項や工程要求事項などを満足することができるか確認することが重要である。これらの評価から得られるデータは計量値(Variable)であるため、プロセスの確認には有用なデータが得られる。具体的な適用可能な統計的手法は以下の通りである:
プロセスバリデーションで使用される統計的手法
| 統計的手法 | 特徴と適用 |
|---|---|
| 仮説検定(平均) | 計量値のデータを用いた平均の仮説検定 |
| 仮説検定(分散) | 計量値のデータを用いた分散の仮説検定 |
| 仮説検定(同等性) | 計量値のデータを用いた同等性の仮説検定 |
| 分散分析 | 計量値のデータを用いた多元配置実験計画 |
| 実験計画法(直交配列) | 計量値のデータを用いた主効果の判定 |
| 二項分布による成功裡の試験 | 計数値のデータを用いたロットの合否判定/試験(Go/No go) |
これらの統計的手法を適切に使用することで、プロセスバリデーションの客観的な評価が可能となる。ただし、得られたデータの性質(計量値か計数値か)や評価目的に応じて、最適な手法を選択することが重要である。