第3章 統計的推定とは

3.1 統計的推定の基本的考え方

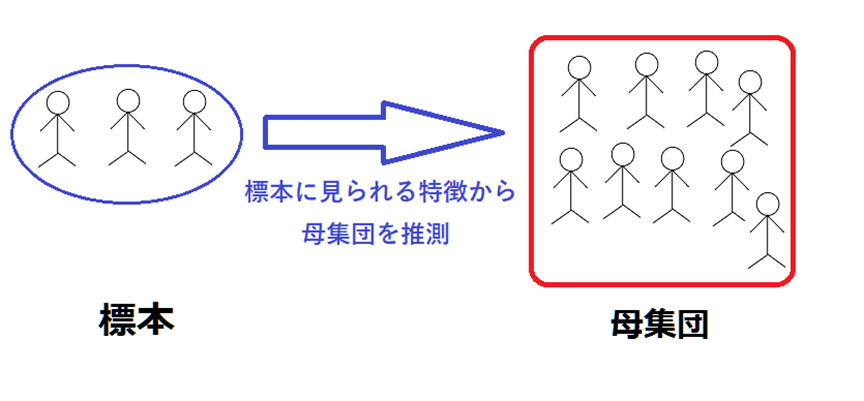
我々が統計をとることができるのは、母集団から無作為に選ばれた標本に対してのみであることが多い。しかし、本当に知りたいのは母集団の性質である。標本の性質をいくら語っても意味がなく、そもそも母集団の性質を調べたいのである。これが我々の本来のゴールであり、このことを忘れてはならない。統計的推定とは、標本の特徴から母集団の性質を推測することである。我々が手にすることができるのは手元にある標本だけであり、このサンプルに見られる特徴から母集団を推測することが求められる。このような手法を用いる統計学を推計統計学、推測統計学、または推計学などと呼ぶ。

3.2 サンプリングの重要性と確率論的性質

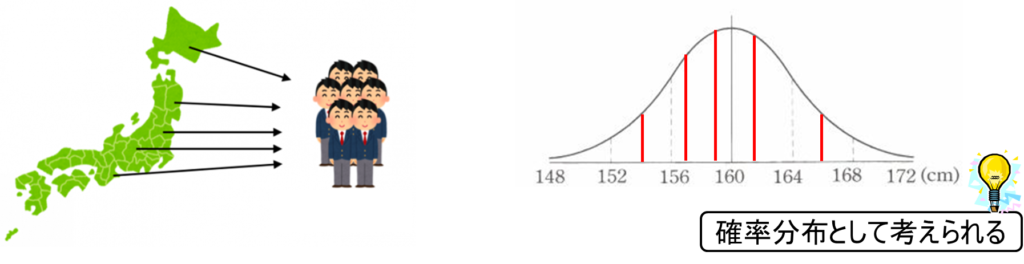
全国の高校生の平均身長を知りたいという例を考えてみよう。このとき、全国なのに青森県の高校生だけを測定するというようなことをすると偏ってしまう。したがって、ランダムに全国からサンプルを抽出しなければならない。全高校生の身長を継続して平均を計算することは現実的に不可能であるため、どうしてもサンプリング（標本）に頼らざるを得ない。

ランダムな無作為のサンプリングは確率論で語ることができる。例えば、1人目をサンプリングしてきたら160.7センチメートルであり、2人目は157センチメートル、3人目は160センチメートル、4人目、5人目、6人目と測定していくと、正規分布に従った分布が形成されていく。この正規分布は160センチメートルが平均である場合、160センチメートル付近を選ぶ確率が最も高くなる。逆に言えば、172センチメートル付近や148センチメートル付近は確率が低くなる。このように、正規分布は確率分布を表しているのである。

母集団が十分に大きい場合、正規分布、つまり平均が一番多いという分布に従うことが知られている。このことから、ランダムなサンプリングは確率論で説明できることが直感的に理解できる。これは統計的推定における重要なキーワードの一つである。

3.3 点推定と区間推定

統計的推定には、点推定と区間推定という二つの推定方法がある。点推定とは、標本から求めるただ一つの値によって母数を推定する手法である。区間推定とは、標本から母数が含まれるであろう区間を推定することである。

例えば、点推定は母平均がここだと、例えば身長は160.1センチメートルというように一つの値をピンポイントで推定する方法である。一方で区間推定は、おそらく158センチメートルから162センチメートルの間だろうというように、この中にあるだろうと範囲で推定する方法である。この標本があり、サンプルがある中で、ここだというのが点推定でピンポイントであり、この範囲だと予測するのが幅で予測する区間推定である。

3.4 信頼度と信頼区間の詳細

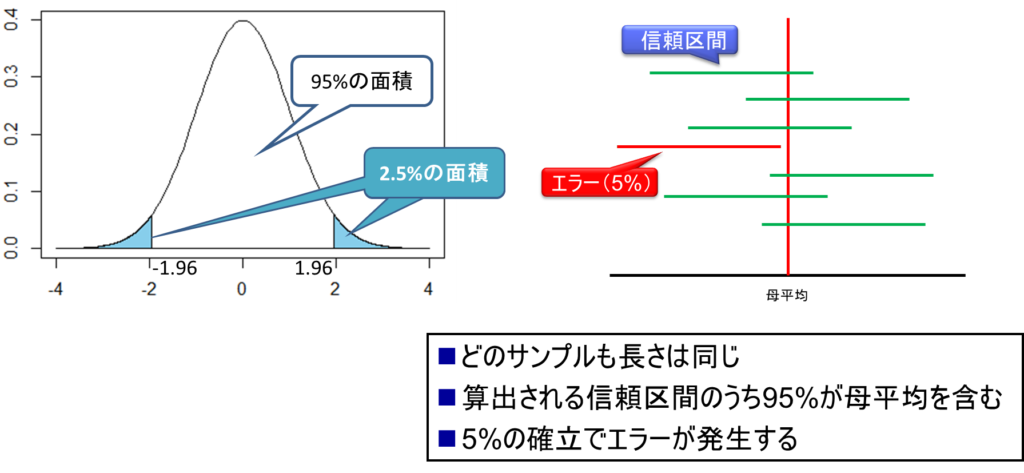
信頼度95%で平均を推定するということをよく耳にする。これは95%の面積、つまり確率論的な考え方に基づいている。95%ということは、両側の片側が2.5%ずつで合計5%となる。この値は正規分布の場合、平均から1.96の位置から外が2.5%、2.5%であることが分布表からわかっている。

この95%の面積が持つ意味について、直感的にわかりやすく説明すると以下のようになる。例えば1回目に全国の高校生からサンプリングをして、その結果、この緑のバーの範囲のどこかに本当の母集団の母平均があるという区間推定を行う。これが信頼区間である。2回目は別の結果になり、3回目、4回目、5回目、6回目というように繰り返していく。

このとき注目すべきことは、ある回の信頼区間は真実を表していない場合がある。つまり、この信頼区間の中に本当の平均、母平均が含まれていない場合があり、これは間違いとなる。ここで重要なことは、全ての信頼区間の長さが一緒だということである。算出される信頼区間のうち95%が母平均を含んでいるのである。

これは言い換えると、100回検定したとすれば5回はミスするということである。逆に言えば95回までは母平均を含む結果になる。これが95%の信頼区間という考え方である。別の言い方をすれば、5%の確率でエラーが発生するということである。

3.5 確率論に基づくサンプリングの特性

ここで強調したいのは、サンプリングは確率論であるため、必ずエラーが入るという点である。つまり、エラーゼロには絶対にならない。どんなにやってもサンプリングは確率的であるため、エラーを含んでしまう。

そこで今日の議論で重要になってくるのは、何%までのエラーなら許容するかという点である。5%のエラーまで認めるのか、それとも1%までしか認めないのかという選択になる。ゼロにはなりえないため、1%にするか5%にするかという判断が必要になってくる。このように統計的推定においては、誤差の許容範囲を適切に設定することが極めて重要である。

3.6 結論

統計的推定は、限られた標本から母集団全体の特性を推測する重要な手法である。点推定と区間推定の二つの手法があり、特に信頼区間を用いた区間推定では、推定の不確実性を定量的に評価することができる。サンプリングには必ず確率的な誤差が伴うことを理解し、その許容範囲を適切に設定することが、信頼性の高い統計的推定を行う上で不可欠である。