第6章 サンプルサイズの決定
6.1 サンプルサイズの決定方法
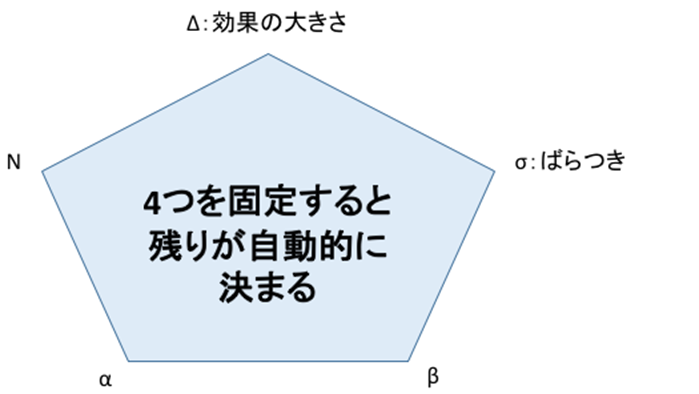
サンプルサイズの決定方法について、結論から述べると以下の4つの値を決定することでサンプルサイズは自動的に定まる。第一に効果量(群間の効果の差)、第二にサンプルの標準偏差(ばらつき)、第三に有意水準(P値、信頼度、αエラーを防ぐ力)、そして第四に検出力(検定力、パワー、βエラーを防ぐ力)である。これら四つの値が決まれば、残りのサンプルサイズは統計ソフトによって自動的に算出される。
実際の手順としては、まず効果量を含めた4つの数値を決定してサンプルサイズを計算し、次に適切なサンプルサイズで実験・調査・検証を実施し、最後に収集したデータを統計解析するという流れとなる。ただし、この段階に至るまでに予備調査や先行研究などによってある程度数値が読めていることが前提となる点に注意が必要である。
サンプルサイズに対する一般的な誤解として、「サンプルサイズは大きい方が良い」という考え方と、「N数を大きくすることは手間なので、なるべくサンプルサイズを小さくしたい」という二つの相反する考え方がある。しかし、これらはいずれも誤りである。「この検証ではちゃんと有意差が出るようにサンプルサイズを大きくしなければ」という考えは適切ではなく、正しくは「何人以上」ではなく「何人」という具体的な数値を決定する必要がある。
サンプル数とサンプルサイズは異なる概念である。サンプル数(the number of samples)とは何回標本抽出を行ったか、群数、標本数のことを指す。一方、サンプルサイズ(sample size)とは1回の標本抽出において何個体を調べたか、各標本、各群の個体数、各群のサイズ、N数を指す。多くの資料やセミナーではサンプルサイズのことをサンプル数と呼んでしまっているが、厳密には異なる概念である。
例えば、がんを発症したマウスに対して、コントロール薬、A薬、B薬(それぞれC群、A群、B群とする)を投薬し、一定時間経過後、腫瘍径の母平均の差を比較する実験を行うとする。実験の予算等の関係でC群、A群、B群それぞれに対して5、7、7個体のデータを取得できた場合、サンプル数(群数)は3であり、サンプルサイズ(各群のサイズ)はC群が5、A群が7、B群が7となる。
すべてのデータ(母集団全体)を把握できない場合、サンプリングが必要となる。全数把握可能なものとしては最終検査、苦情管理などがあり、サンプリングが必要なものとしては購入したネジ100万本の受入検査、ある工作機械で製造する製品のばらつきなどがある。液体など、ばらつきのないものに関してはN=1で構わない。例えば、よく混ぜた味噌汁は上澄みを取ろうが真ん中を取ろうが鍋底を取ろうが全て同じ味になるため、どこを取っても同じ値を代表する。したがって、サンプルサイズは1で十分である。

6.2 有意差ありとは
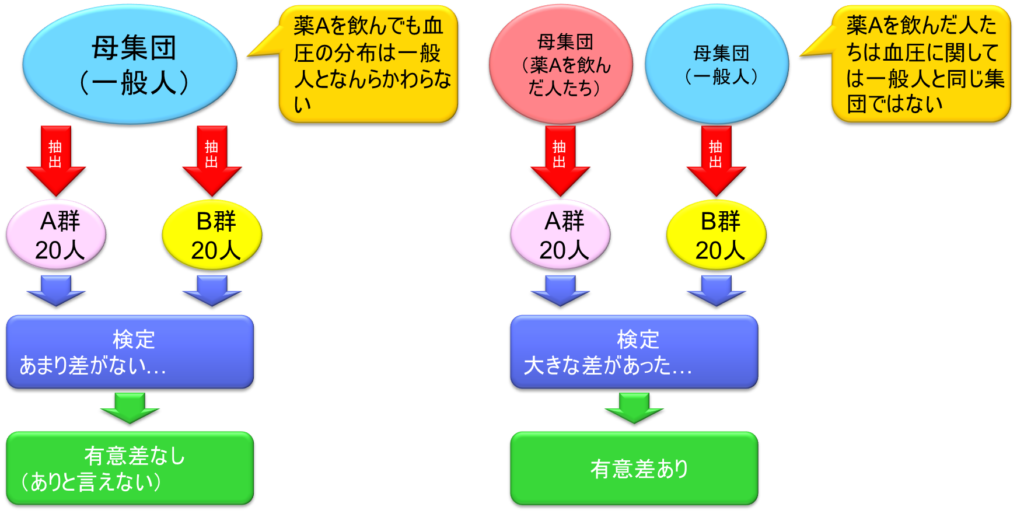
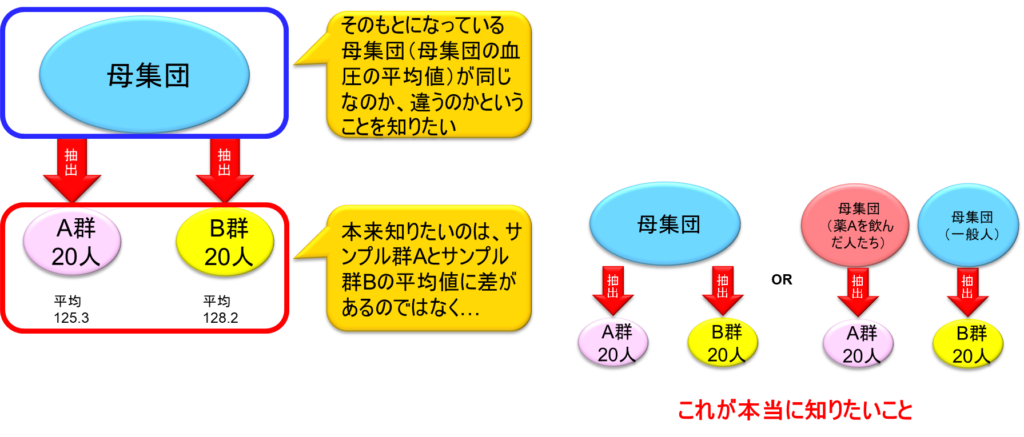
例えば、血圧を下げる薬Aがあるとして、被験者40人を2群に分ける。A群は薬Aを飲んだ人たち20人、B群は偽薬(プラセボ)を飲んだ人たち20人である。この2群の人たちの血圧を測って両群の平均値を比べる。その上で有意な差があるかどうかを検定する。有意差ありとなった場合、両群の血圧には差があるという結論となり、逆に有意差なしとなった場合は、両群の血圧には差がない、または少なくとも両群の血圧に差があるとは言えないという結論となる。
しかし、ここで重要なのは、我々が本当に検定したいのは、この薬を飲んだ人たち20人またはプラセボを飲んでない人たち20人の差を知りたいわけではなく、そもそものA群とB群の母集団の差を知りたいという点である。正確には、有意差ありというのは、両群の母集団の血圧に差があるということを結論として言いたいのであり、有意差なしとしているのは、両群の母集団の血圧には差がない、差があるとは言えないということを言いたいのである。サンプルを論じるのではなく、母集団を論じないといけない。それがゴールだということを忘れてはならない。

6.3 第1種の過誤と第2種の過誤
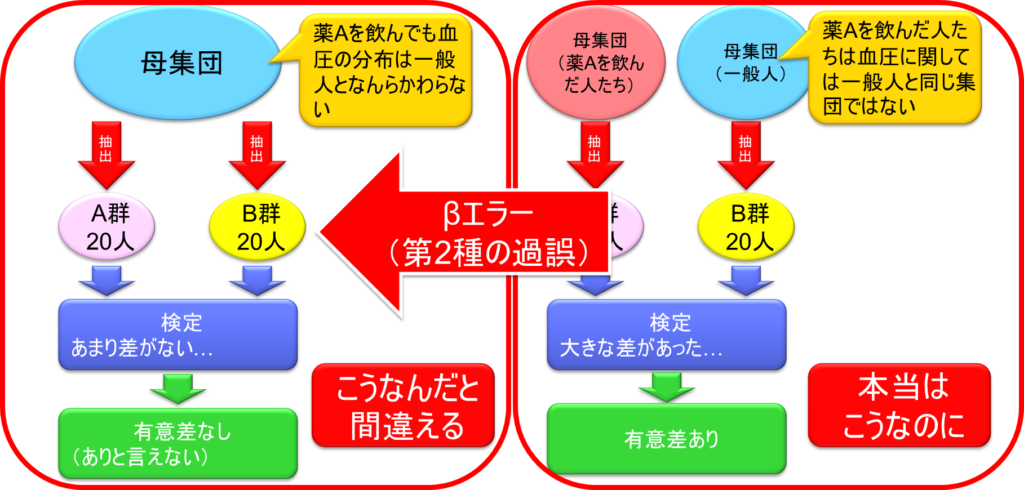
ここで問題があるのは、A群薬を飲んだ後20人とB群20人の値しか手元にないということである。母集団のデータはそもそも手元にない。これを検定したとき、あまり差がないという結論になったとする。要するに有意差なし、少なくとも有意差があるとは言えないという結論が統計ソフトから返ってくる。統計ソフトが扱った与えられたデータはA群20人とB群20人だけである。しかし、その結果から推察されることは、A群とB群はおそらく同じ母集団から採取してきたのだろうということである。これは結論として、薬を飲んでも血圧の分布は一般人と何ら変わらないということになる。
一方で、A群20人とB群20人で検定をしたときに大きな差があったという結論になった場合、すなわち有意差ありという結論になった場合、このサンプリングから有意差があると結論づけられたということは、母集団はおそらく異なっているだろうということが推察される。A群は母集団として薬を飲んだ人たちを代表しており、B群は一般人を代表しているということとなる。つまり、薬を飲んだ人たちは血圧に関しては一般人と同じ集団ではないという結論に至るということである。
6.4 第1種の過誤と第2種の過誤(αエラーとβエラー)
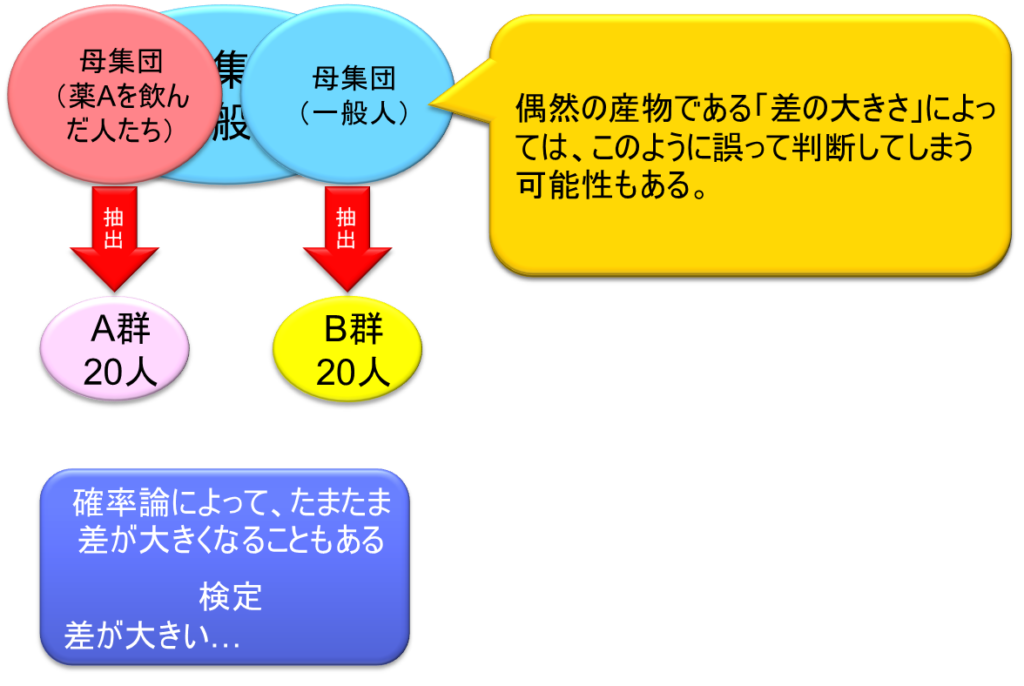
同じ母集団からA群とB群を抽出してきた場合を考える。この場合、A群とB群で血圧の平均値が全く完全に一致するということはそれはそれで珍しい。お互いにランダムに抽出できているから、若干の差が生じるのが普通である。必ずこれは差が出るわけである。大抵は小さな差の場合もあれば、場合によっては大きな差があることも普通である。確率論によってたまたま差が大きくなることもある。検定をしたときに差が大きいという結論になってしまうと、本当はこうだったのに、たまたまサンプリングがまずくて差が大きくなってしまい、結果的にこうではないかという間違った評価になってしまうこともありうるのである。これは確率論であり、確率的にありうることである。
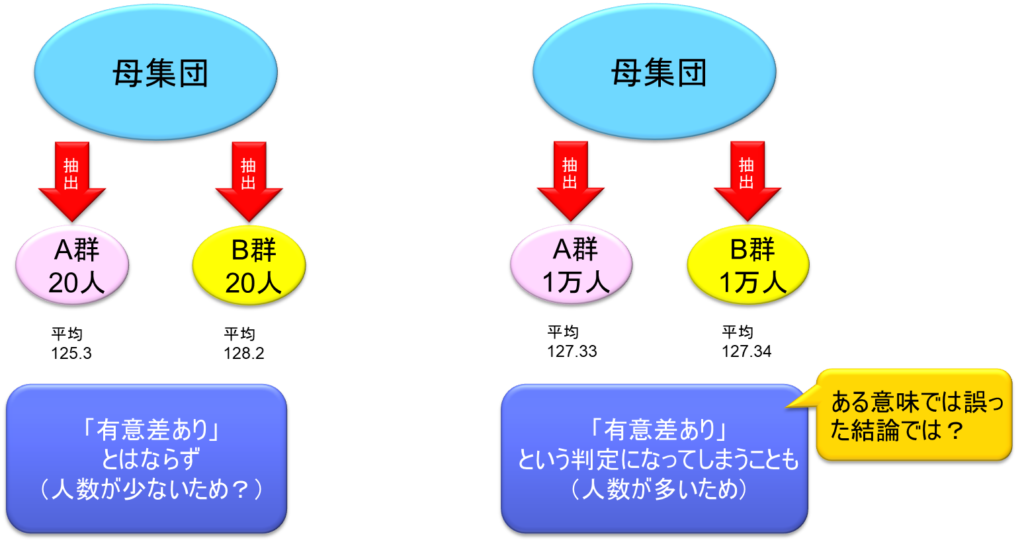
また、サンプリングのサイズについても考える必要がある。例えば母集団から二つのサンプリングを行う。一つは20人ずつのサンプリング、もう一つは1万人ずつのサンプリングである。20人ずつの場合、平均が125.3と128.2というように明らかに平均が離れている場合でも、人数が少ないためこれだけの差では有意差ありとはならないのである。一方で1万人ずつ集めた方を見ると、平均が127.33と127.34という小数点2桁目でやっと差がついているような場合でも、これだけの差があれば有意差ありという判定になってしまうことがある。これは人数が多いために有意差ありとなってしまうのである。これはある意味で誤った結論になってしまうということである。

6.5 なぜサンプルサイズを決定しなければならないのか
サンプルサイズを決定しなければならない理由は、第一種の過誤(αエラー)を犯さないためには、ちょっとの差では「有意差あり」と判断しないようにブレーキをかけるような方向性で検定をしなければならないからである。そのためにはP値の基準を厳しくする必要があり、サンプルサイズを小さくする方向、すなわち有意差が出にくい方向にブレーキをかけなければならない。
一方で、第二種の過誤(βエラー)を犯さないためには、小さな差を見落とさず有意差ありと言えるような方向性を持っていかなければならない。これは検出力を高める方向であり、そのためにはサンプルサイズを大きくする方向、すなわち有意差が出やすい方向に持っていく必要がある。しかし、この上下はトレードオフの関係にあり、どちらも成り立つということはできない。適切なバランスのあるところを、サンプルサイズとして決めなければならない。
サンプルサイズを事前に決めないと、なぜP値が小さくなったのかがわからなくなる。その理由として、群間の差が大きくてP値が小さくなった可能性と、サンプルサイズが大きくてP値が小さくなった可能性の二つがある。検定には、サンプルサイズが大きいと有意差が出やすい(T統計量が大きくなる、つまりP値が小さくなる)という特性と、サンプルサイズが小さいと有意差が出にくいという特性がある。
6.6 サンプルサイズ検討に必要な情報
サンプルサイズを検討するためには、以下の情報が必要となる。まず何が知りたいのか、平均値なのか、ばらつきなのか、母集団はいくつあるのか、計量値か計数値かを決定する必要がある。次に帰無仮説(対立仮説)が何か、イコール(≠)なのか、小なり(<)なのか、大なり(>)なのかを決める必要がある。さらに母集団の統計量として、平均値、標準偏差(既知か未知か)を把握する必要がある。最後に第一種の誤り、第二種の誤りについて、αは1%、5%、その他、βは10%、20%、その他といった具体的な数値を決定する必要がある。
6.7 サンプル評価のステップ
サンプル評価は以下の手順で進める:
- 知りたいことを定義する
- 一つの母平均の検定を行いたい
- 一つの母分散の検定を行いたい
- 二つの母平均の差を検定したい
- その他
- 仮説および対立仮説を立てる
- 同じである(≠)
- 大きい(<)
- 小さい(>)
- サンプルサイズを近似する
- 検出力を確認する
- サンプルサイズを決定する
- サンプルを作成する
- ランダムサンプリングを行う
- 試験・評価を行う
- 検定を実施する
- 区間推定するためのサンプルサイズを決定する
- サンプルを測定する
- 区間推定を行う