第9章 検出力とは

9.1 検出力（Statistical Power）の基本概念

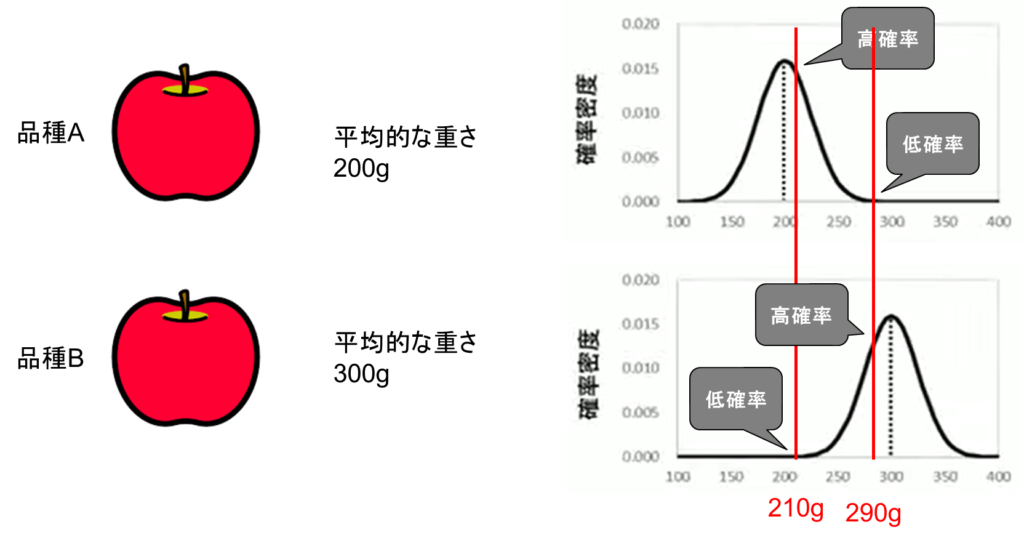
統計的仮説検定では、ある仮説を立てて、その仮説が統計的に成り立つか否かを確率を用いて判断する。例として、品種Aのリンゴは平均的な重さが200gで、品種Bのリンゴは平均的な重さが300gである場合を考えてみよう。個体差があるため、リンゴの重さはそれぞれ200gと300gを中心として広がりを持った正規分布となる。

今、目の前に1つのリンゴがあり、その重さを量ったところ210gであったとする。このリンゴは品種Aであろうか、それとも品種Bであろうか。このグラフを見ると、かなりの確率で品種Aであると判断できる。なぜならば、このリンゴが品種Aであると仮定したときに210gが観測される確率は高く、品種Bであると仮定したときに210gが観測される確率は低いからである。しかし、このリンゴが品種Bである確率は完全に0%ではない。210gの品種Bのリンゴはかなり低確率ではあるが、観測されうるのである。

次に、別のリンゴの重さを量ったところ290gであったとする。この場合、このリンゴは品種Bである可能性が高いと判断できる。なぜならば、このリンゴが品種Bであると仮定したときに290gが観測される確率は高く、品種Aであると仮定したときに290gが観測される確率は低いからである。しかし、このリンゴが品種Aである確率は完全に0%ではない。290gの品種Aのリンゴはかなり低確率ではあるが、観測されることがありうるのである。

このように、統計的仮説検定では仮説が正しいかどうかを統計的に判断するが、その判断が100%正しいということはない。判断と事実が異なる可能性が常に存在するのである。

9.2 第一種の誤りと第二種の誤り

統計的仮説検定で起こりうるのは以下の四つのパターンである。統計的仮説検定で立てる仮説のことを帰無仮説と呼ぶ。

第一のパターンは、実際は帰無仮説が正しい時に、帰無仮説が正しいと判断する場合である。第二のパターンは、実際は帰無仮説が正しい時に、帰無仮説が正しくないと判断する場合である。第三のパターンは、実際は帰無仮説が正しくない時に、帰無仮説が正しいと判断する場合である。第四のパターンは、実際は帰無仮説が正しくない時に、帰無仮説が正しくないと判断する場合である。

この中で判断が正しかったのは第一と第四のパターンである。判断が誤っていたのは第二と第三のパターンである。ここで、この二つの判断の間違いは、その性質が異なっている。第二のパターンは帰無仮説が正しいにもかかわらず、帰無仮説が誤っていると判断してしまっており、第三のパターンは帰無仮説が誤っているにもかかわらず帰無仮説が正しいと判断してしまっている。

第二のような誤りを第一種の誤りと言い、発生確率を通常αで表現する。第三のような誤りを第二種の誤りと言い、通常発生確率をβで表現する。統計的仮説検定では通常、帰無仮説が誤っていることを主張することを目的とする。つまり、帰無仮説を棄却することによって対立仮説が正しいということを主張することが目的である。

9.3 検出力の定義

対立仮説が正しい場合に、それを正しく判断できる確率は1からβを引いたもの、すなわち1-βとなる。この1-βは実際に帰無仮説が誤っている場合に、帰無仮説が誤っていると正しく統計的に判断できる確率のことであり、これを検出力（パワー）と呼ぶ。

9.4 コイン投げの具体例による検出力の説明

通常のコインは表が出る確率が0.5、裏が出る確率も0.5である。一方、イカサマコインは表が出る確率が0.9で、裏が出る確率は0.1となっているとする。

今、目の前にあるコインがイカサマコインなのか通常のコインなのかを、統計的仮説検定で判断したい。帰無仮説が誤っているときに成立している仮説のことを対立仮説というが、通常のコインであるとするのを帰無仮説とすると、対立仮説の方はイカサマコインであるということになる。

検定では、帰無仮説の矛盾を主張することで間接的に対立仮説の妥当性を主張するというアプローチをとる。よってこの状況では、このコインが通常のコインであるというのを帰無仮説とし、イカサマコインであるという方を対立仮説として設定する。

コインを10回投げた場合、表が出る回数の確率分布は、通常のコインとイカサマコインで異なる分布となる。帰無仮説を棄却するのか受容するのかを判断するには、閾値を決める必要がある。仮に9回以上表が出た場合に帰無仮説が誤っていると判断することにする。これは棄却域と呼ばれ、表が9回以上出たら、これは帰無仮説を棄却して、通常のコインではなくイカサマコインであると判定することになる。

このように帰無仮説が誤っていることを主張できる領域のことを棄却域と呼ぶ。棄却域が9以上の場合、表が出た回数が9回だった場合と10回だった場合は、帰無仮説が棄却されてイカサマコインであると判断されることになる。

ただし、通常のコインであったとしても、10回中9回表が出ることもありうる。稀に偶然ではあるが、10回中10回表が出る確率もある。これがこの確率分布から見ると、9回出る確率が0.010で10回出る確率は0.001である。ゼロではないのである。これを足し合わせると0.011となる。つまり、9回出るかまたは10回出る確率は1.1%存在する。

これは何を表しているかというと、帰無仮説が正しいにもかかわらず、帰無仮説が誤っていると判断しているということである。よってこれは第一種の誤りとなり、その確率は0.011であるということが言える。

9.5 棄却域の設定と検出力の関係

今度は逆に、表の出た回数が0から8回だった場合を考えよう。これは帰無仮説が棄却されず、イカサマコインであるとは言えないという判断になる。しかし、イカサマコインであったとしても表が0回から8回出ることもありうる。イカサマコインは9回や10回出る確率が高いが、0から8回の確率も低いながら存在する。この確率は0.264となる。これは帰無仮説が誤っているにもかかわらず帰無仮説が正しいと判断しているので、第二種の誤りとなる。

ここで目論見通りに帰無仮説が棄却されたときに、その判断が正しい確率は9回と10回の確率を足して0.736となる。この確率は1からβを引いたものが残りとなるため、1-βで表される。この確率のことを検出力と呼ぶのである。

次に棄却域を8以上と設定した場合を考えてみよう。第一種の誤りの確率αはこの部分を足し込むと0.054となる。第二種の誤りの確率βはこの部分を足し込んで0.070となり、検出力1-βは0.930となる。

この結果からもわかるように、αが変わるとそれに連動して、βや検出力も変わることがわかる。つまり棄却域をどう設定するかで、同じ観測結果が得られたとしても、統計的仮説検定での判断が変わってしまうのである。

9.6 連続型確率分布における検出力

次に連続型の確率分布の場合について考えてみよう。先ほど例に挙げた品種Aのリンゴの重さの分布が平均200g、標準偏差25gの正規分布であり、品種Bのリンゴの重さの分布が平均300g、標準偏差25gの正規分布であるとする。

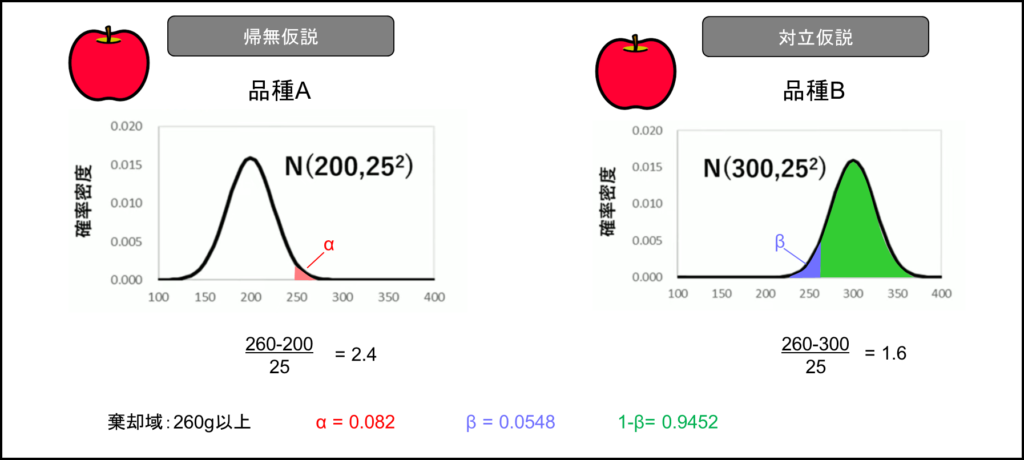
目の前のリンゴが品種Bかどうかを統計的仮説検定で判断したい状況である。品種Aであるというのを帰無仮説とし、品種Bである方を対立仮説とする。棄却域を260g以上とした場合、第一種の誤りの確率αはこの部分の面積となる。第二種の誤りの確率βは別の部分の面積となる。

これらを260gを標準化した上で正規分布表で読み取ると、αは0.0082、βは0.0548という値が得られる。検出力は残りの部分の面積となるため、1からβを引いた部分となり、1-0.0548で0.9452と求めることができる。このように連続型確率分布でも離散型確率分布（計数値）と同じような考え方で、第一種の誤りの発生確率α、第二種の誤りの発生確率β、検出力1-βを求めることができるのである。

9.7 検出力の重要性

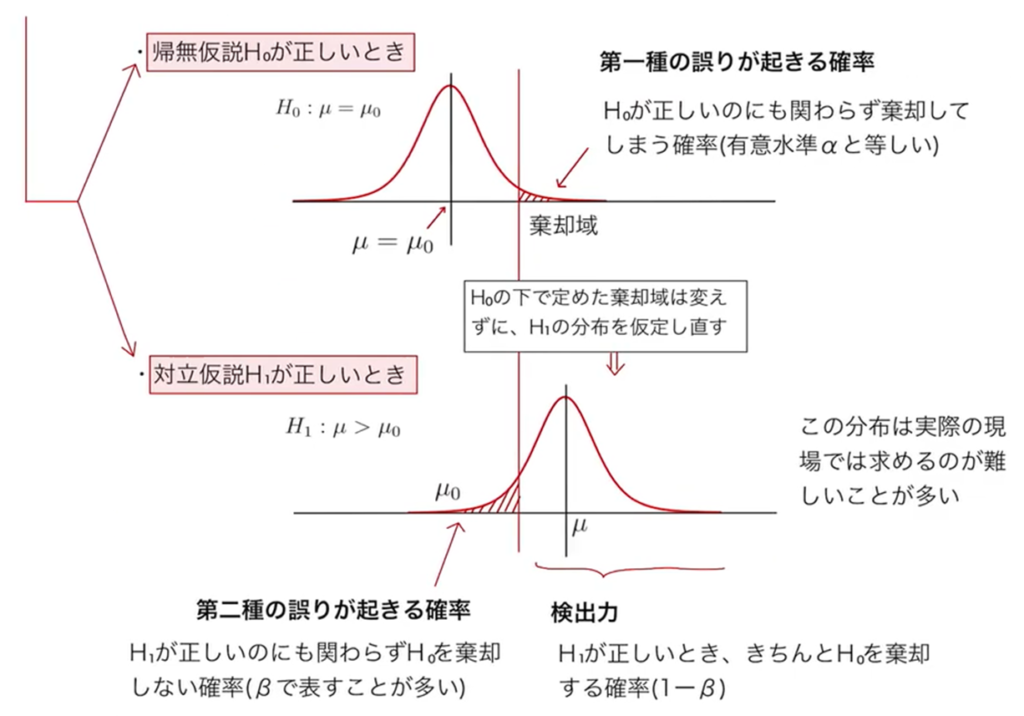
帰無仮説H0が正しいときに第一種の誤りが起きる確率は、棄却域における帰無仮説H0が正しいにもかかわらず棄却してしまう確率であり、これは有意水準αに等しくなる。H0のもとで定めた棄却域は変えずに、対立仮説H1の分布を仮定し直すと、第二種の誤りが起きる確率はH1が正しいにもかかわらずH0を棄却しない確率となる。これがβである。このβを引いた残りの面積1-βが検出力となる。すなわち、H1が正しいときにきちんとH0を棄却する確率が1-βとなるのである。

9.8 設計開発における検出力の意義

消費者危険が受容可能な設計を行うということは極めて重要である。設計開発では、製品工程の品質・安全性を構築して患者・医療施設・ユーザーが安全に使用できるようにする必要がある。そのために設計開発の各段階でリスクマネジメントを実施することが要求されている。

サンプルによる評価でも、消費者に安全で高品質な製品・サービスを提供できることを保証しなければならない。そのときに消費者危険αが意図した基準1-β内にあることを保証する必要がある。この1-βのことを検出力と呼ぶのである。

9.9 実践的な検出力の設定

検出力は1-βという式が成り立つ。検出力が低いということはβが大きいということであり、これは消費者にとって不利になることを意味する。検出力が低いということは、本当は治療効果に違いがあるのに、統計学的検定で有意差が出る確率が低いということである。

通常、検出力は80%に設定することが一般的である。これは本当に治療間で違いがある場合に、10回試験をやったら8回は有意差が出ることを期待するという意味である。

9.10 検出力を高める方法

検出力を高める方法は二つある。一つは有意水準を変更して検出力を高める方法であり、もう一つはサンプルサイズを大きくして検出力を高める方法である。

まず、有意水準を変更して検出力を高める方法であるが、この方法は使用することができない。なぜなら有意水準は5%が鉄則であり、変更することは認められていないためである。医療系の分野で仮説検定を行う場合、有意水準は5%に設定されることが一般的である。これを変更することはできない。

したがって、検出力を高めるためにはサンプルサイズを大きくすることが唯一の方法となる。以下に具体例を用いて、二項検定によるαエラーの事例を説明する。

今、従来はリハビリによる改善率が20%程度の障害に対して、新しい方法で改善率が高まると考えているとする。この新しい方法を10人に試して、改善率が良化しているかを検証することにした。結果は改善か否かの二値であるため、二項分布が使用できる。悪化することはないと考えて片側検定を行うとすると、帰無仮説は「母改善率は20%を上回らない」となる。

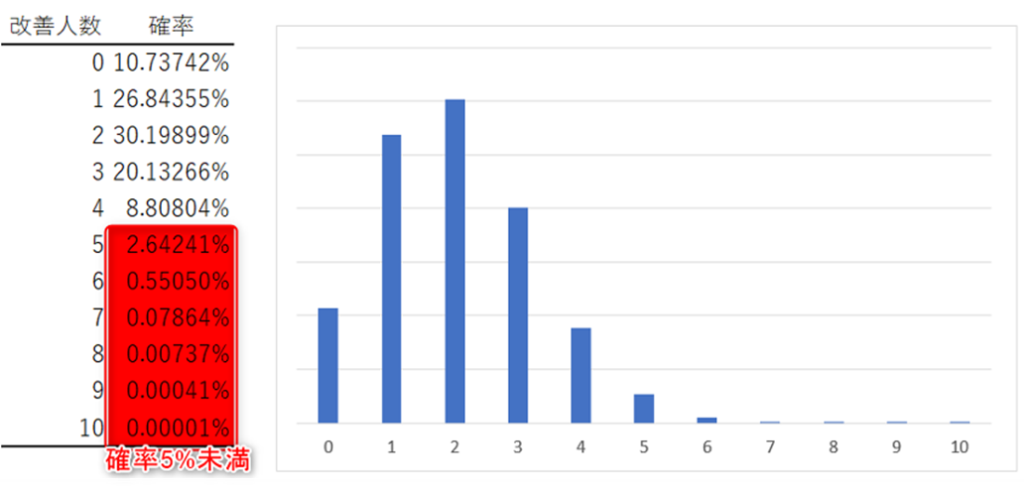
10人の結果について、帰無仮説の上限である20%を用いて二項分布で確率を計算すると、1人から3人程度に改善が見られる確率が高くなっている。改善人数が5人以上になる確率は約3.28%である。4人の改善も含めると確率は10%を超える。有意水準を5%に設定するならば、10人中5人以上の改善で有意水準を下回るので帰無仮説が棄却されることになる。この場合は約3.28%のαエラーを許容することになる。

帰無仮説「母改善率は20%を上回らない」に対する対立仮説は「母改善率は20%を上回る」である。「母改善率は20%を上回る」という仮説には、母改善率が20%を超えて100%まであらゆるケースが含まれる。

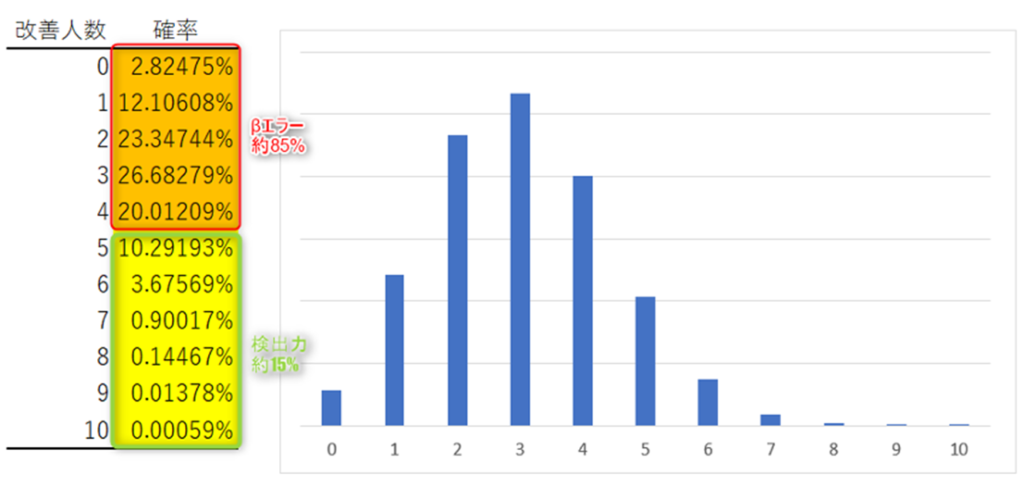
仮に真の母改善率が30%だとすると、10人に試した場合の改善人数の確率は以下のようになる。有意水準5%のもと、帰無仮説を前提にした棄却域は前述の通り5人以上の改善である。その場合、真の母改善率を30%とすると、約85%の確率で改善人数が5人未満となる。すなわち、85%の確率で帰無仮説を棄却できないことになる。この85%がβエラーである。逆に約15%の確率で改善人数が5人以上となる。すなわち15%の確率で帰無仮説を棄却できることになる。この15%が検出力である。

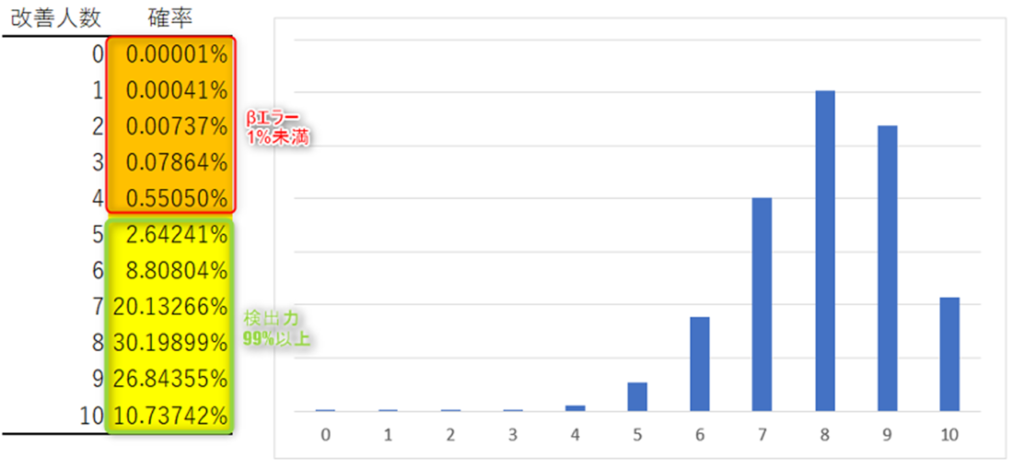
次に、真の母改善率がもっと高く80%だった場合を考える。10人に試した場合の改善人数の確率分布は大きく異なってくる。この場合、改善人数が5人未満となり帰無仮説を棄却できない確率は1%未満になる。すなわちβエラーは1%未満である。それに対して、改善人数が5人以上となり帰無仮説を棄却できる確率（検出力）は99%以上となる。

このように、検出力は真の母数が帰無仮説の値と乖離していればいるほど高くなる。つまり、大きな差があるものほど、より正しく検出できるということである。

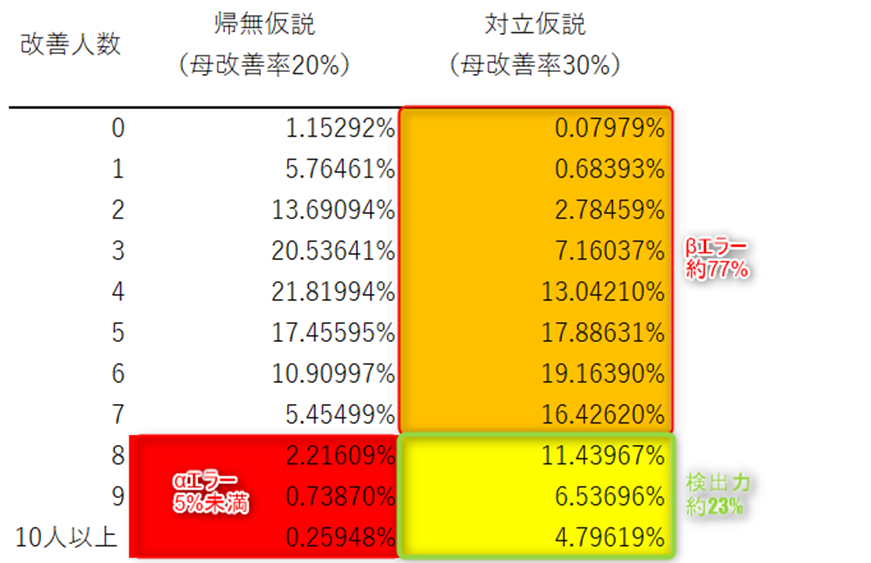
被験者を10人から20人に増やした場合を考えてみよう。帰無仮説の母改善率20%を前提に確率を求めると、改善人数が8人以上で5%を下回り、帰無仮説は棄却されることになる。対立仮説の方を真の母改善率が30%であるとした場合、改善人数が8人未満になる確率（βエラー）は約77%となる。改善人数が8人以上となる確率（検出力）は約23%なので、検出力が被験者10人のときに比べて0.05程度向上していることが確認できる。

このように、サンプルサイズを大きくすると検出力が高くなる。このことを利用して、サンプルサイズの計算を行うことが重要である。