第7章 帰無仮説とは

7.1 背理法による仮説検定の基本概念

統計的手法において、帰無仮説という考え方は極めて重要である。まず、立てた仮説の正しさを証明することは非常に困難である一方で、仮説が正しくないことを証明することは可能である。この考え方を理解するために、具体的な例を見てみよう。

「この世のすべてのカラスは黒い」ということを証明することを考えてみる。これを証明するためには、世界中に生息するすべてのカラスを観察して黒いことを確かめなければならない。これは現実的には不可能な作業である。つまり、仮説が正しいことを証明することは極めて困難なのである。

7.2 第1種の過誤と第2種の過誤

このような状況に対処するため、統計的仮説検定では背理法という考え方を採用している。ここで重要なのは、重大な誤りを第1種の過誤として扱うということである。具体例として、ある製薬メーカーが従来よりも効果をアップさせた新薬を開発した場合を考えてみよう。実験によってその効果を観測し、検定で判断をする際には、二つの誤りが発生する可能性がある。

第1の誤りは、薬の効果アップが実際にはあるのに、無いと判断してしまうことである。これを第1種の過誤、すなわち生産者危険あるいは「あわて者の誤り」と呼び、通常αで表す。一般的にα=5%と設定されることが多い。

第2の誤りは、薬の効果アップが実際には無いのに、あると判断してしまうことである。これを第2種の過誤、すなわち消費者危険あるいは「ぼんやり者の誤り」と呼び、通常βで表す。一般的にβ=20%と設定されることが多い。

7.3 帰無仮説の概念と特徴

背理法による仮説検定の大きな利点は、第1種の過誤を犯す確率を、有意水準として自分で設定できることである。この設定により、統計的な判断の精度をコントロールすることが可能となる。

統計的仮説検定において、帰無仮説（null hypothesis）とは、検定の際にとりあえず立てる仮説のことである。これは記号「H₀」として表されることが多い。重要な点として、実際には対立仮説の方が重要であることが多いという特徴がある。

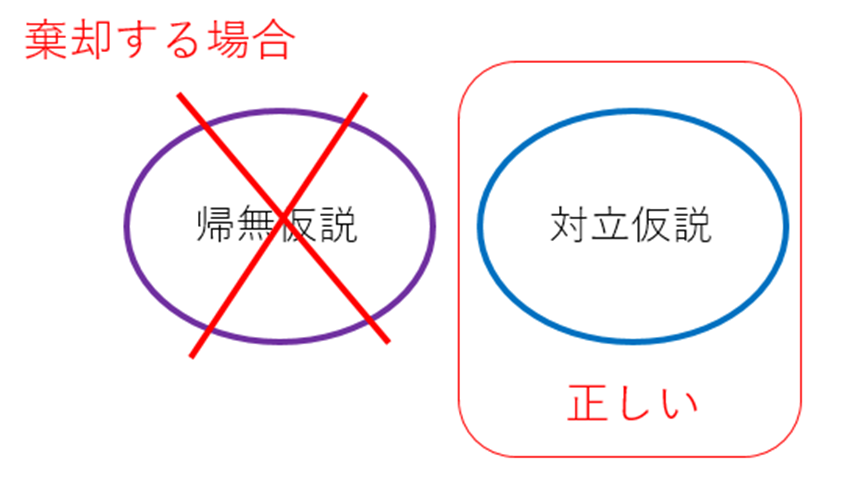
例えば、帰無仮説として「差がない」という仮説を立てた場合を考えてみよう。この帰無仮説が棄却されることによって、対立仮説である「差がある」という結論を導くことができる。これは間接的な証明方法であり、帰無仮説を否定することで対立仮説の妥当性を主張するというアプローチである。

7.4 帰無仮説の棄却と解釈

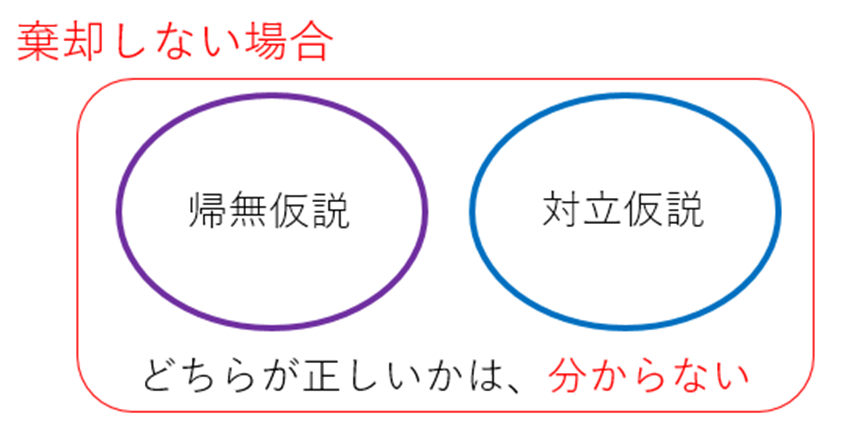
ここで特に注意しなければならないのは、「帰無仮説を棄却しない」ということは「帰無仮説を受容する」ということとは異なるという点である。帰無仮説を棄却しないということは、必ずしも帰無仮説が正しいということを意味しない。言い換えれば、帰無仮説を棄却できなかった場合、帰無仮説が正しいのか対立仮説が正しいのかは判断できない状態となる。

このため、統計的仮説検定では、帰無仮説を棄却して対立仮説が正しいということを証明することが重要となる。これにより、検定の結果に基づいて明確な結論を導くことが可能となる。この考え方は、医療機器の開発や品質管理において、製品やプロセスの有効性や安全性を科学的に実証する上で極めて重要な役割を果たしている。