第2章 統計的手法の基礎

2.1 データの構造

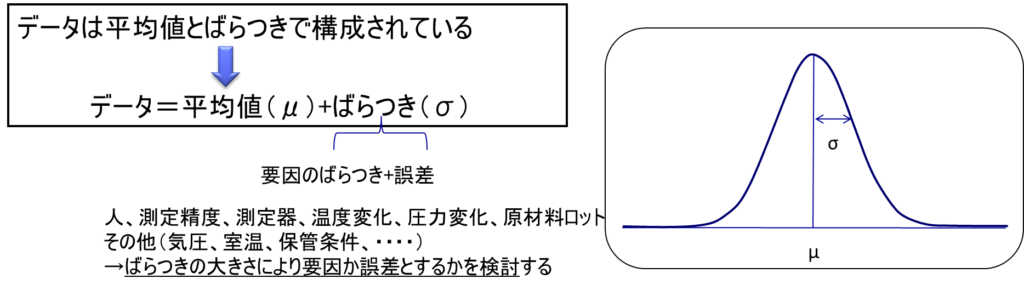
データは平均値とばらつきという二つの要素で構成される。数式で表現すると、データ = 平均値(μ) + ばらつき(σ)となる。例えば、A薬品100.0グラムを秤量した結果は、平均値に秤量のばらつき、秤のばらつき、その他のばらつきが加わったものとなる。同様に、A薬品を純水に溶解したC溶液濃度は、平均値にA薬品量のばらつき、純水のばらつき、計測のばらつき、その他のばらつきが加わったものとなる。

ばらつきは要因によるものと誤差によるものに分類できる。ばらつきを生じさせる要因としては、人的要因、測定精度、測定器、温度変化、圧力変化、原材料ロット、その他の環境要因（気圧、室温、保管条件など）がある。これらのばらつきの大きさによって、それが要因として扱うべきものか、あるいは誤差として扱うべきものかを検討する必要がある。

2.2 計量値と計数値の分布

データには大きく分けて計量値と計数値という二種類がある。計量値は分布が連続した値をとることができるものを指す。計量値の例としては、重さ、長さ、電圧、速度などが挙げられる。このような計量値は母集団において正規分布に従い、そこからサンプリングを行った場合はt分布に従うことが知られている。

一方、計数値は分布が連続した値を示さないものを指す。例えば、サイコロの目のように1から6までの離散的な値しか取り得ないものや、不良率、個数、有無などが該当する。計数値は二項分布に従う。さらに、計数値の中でも不適合の発生が十分に小さいと考えられる場合（例えば事故発生率や故障率など）は、ポアソン分布に従うことが知られている。

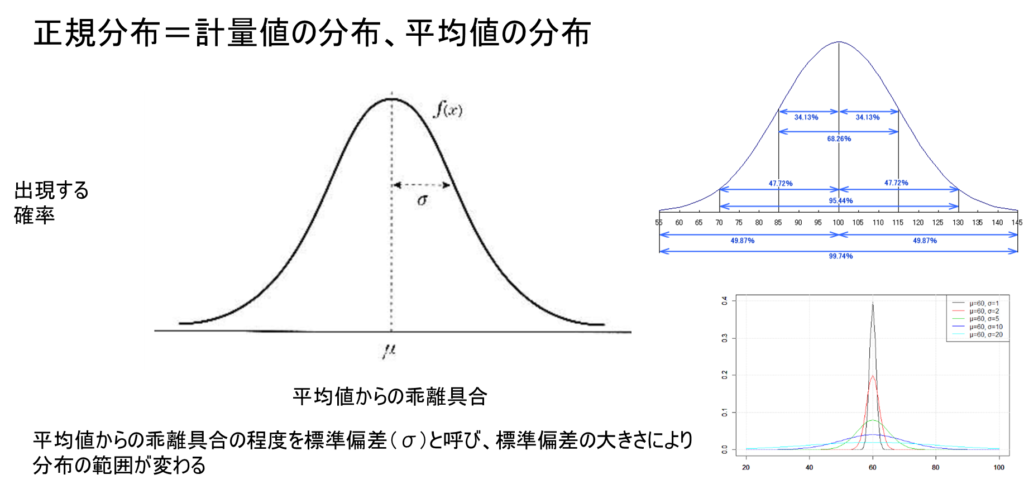
2.3 計量値の分布：正規分布

正規分布は、平均値を中心として左右対称な釣鐘型の分布を示す。平均値からの乖離具合の程度を表す指標として標準偏差(σ)が使用され、この標準偏差の大きさによって分布の範囲が変化する。

正規分布において、平均値から標準偏差(σ)の範囲内には全体の約68.26%のデータが含まれ、2σの範囲内には約95.4%、3σの範囲内には約99.74%のデータが含まれることが知られている。標準偏差が大きくなるほど分布は横に広がり、なだらかな山型となる。逆に標準偏差が小さくなるほど、分布は中心に集中し、急峻な山型となる。

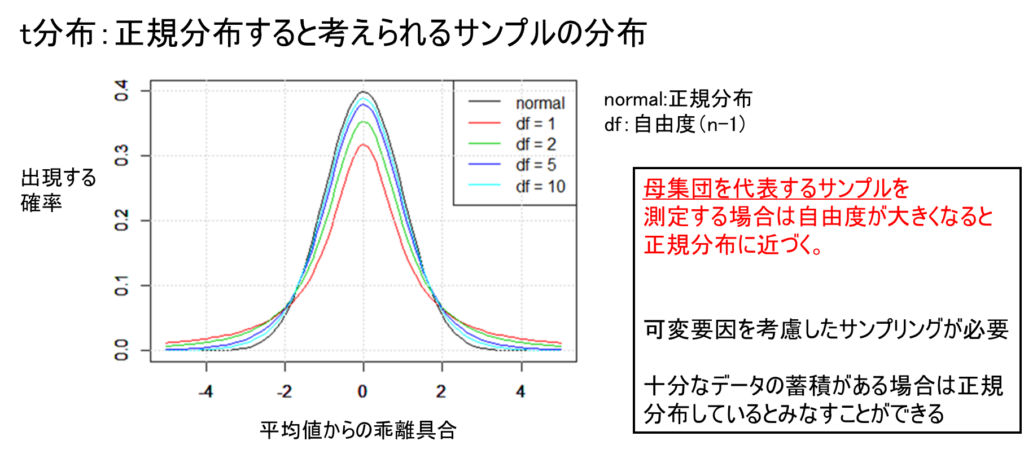
2.4 計量値の分布:t分布

t分布は、正規分布からサンプリングを行った際のサンプルの分布を表す。t分布は正規分布に似た形状を示すが、裾野がやや広がった形状となる。このt分布は自由度（サンプルサイズNから1を引いた値）によって形状が変化する。

母集団を代表するサンプルを測定する場合、自由度が大きくなるにつれてt分布は正規分布に近づいていく。このため、十分なデータの蓄積がある場合は、そのデータは正規分布していると見なすことができる。サンプリングを行う際には、可変要因を考慮したサンプリング方法を採用する必要がある。

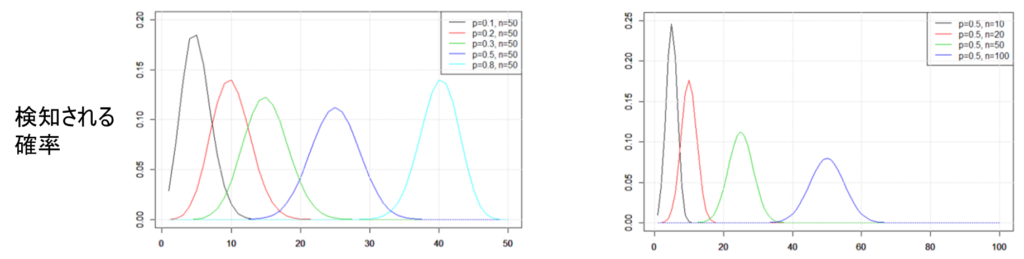
2.5 計数値の分布：二項分布

二項分布は、不良率がpの母集団からn個の抜き取りを行った場合に検出される不良数とその確率を表す分布である。この分布には以下のような特徴がある：

１．ロットの不良率が一定であっても、抜き取り数により検知される不良数は変化する。

２． 抜き取り数が一定であっても、ロットの不良率により検知される不良数は変化する。

３．サンプルサイズnを大きくすると、分布は正規分布に近似できるようになる。

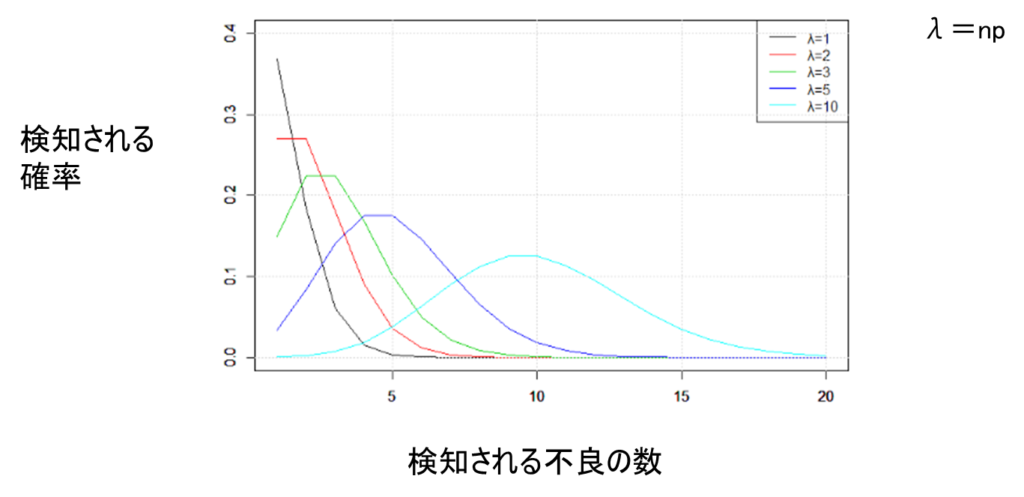
2.6 計数値の分布：ポアソン分布

ポアソン分布は、二項分布において不適合の発生が十分に小さい場合（例えば事故発生率や製品故障率など）に適用される分布である。この分布の特徴として、以下の点が挙げられる：

１．ロットの不良率が一定であっても、抜き取り数により検知される不良数は変化する。

２．抜き取り数が一定であっても、ロットの不良率により検知される不良数は変化する。

３．λ(=np)が10以上となるサンプルサイズnでは、正規分布に近似できる。

2.7 分布の違いによる確率密度関数式

各分布タイプにはそれぞれ固有の確率密度関数式が存在する。ただし、実際の現場では各分布の分布表もしくは表計算ソフトを用いることが多いため、これらの関数式を暗記する必要はない。

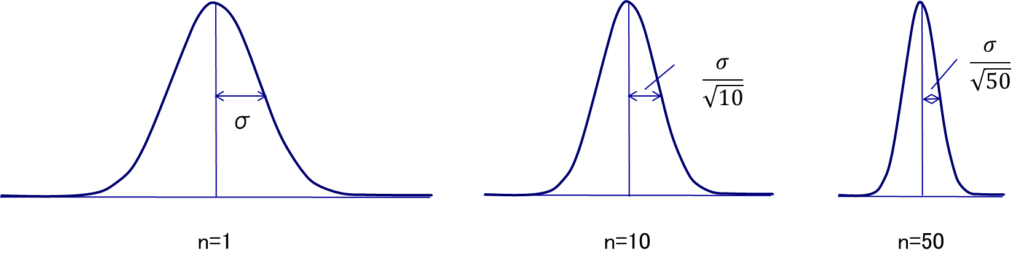
2.8 サンプルサイズ決定の基本原則

任意の分布から得られた平均値の分布は正規分布を示す。この際、平均値のばらつきは、元となるサンプルサイズが大きくなるにつれて1/√n倍に縮小していく。例えば、サンプルサイズが1の場合に比べて、サンプルサイズが10の場合は1/√10倍に、50の場合は1/√50倍にばらつきが減少する。これは、サンプルサイズを増やすことで、より母集団の特性を正確に推定できるようになることを示している。