第10章 サンプルサイズ、検出力の計算式

本章では、一つの母平均の検定におけるサンプルサイズの検討から始め、様々なケースにおけるサンプルサイズと検出力の計算式について解説する。実際には、パソコンの統計ソフトを用いて計算を行うことが一般的であるが、統計ソフトの中でどのような計算が行われているかを理解するために、各ケースにおける計算式を詳しく説明する。

10.1 一つの母平均の検定におけるサンプルサイズの検討（母分散既知の場合）

一つの母平均の検定における母分散が既知の場合のサンプルサイズの検討について説明する。対立仮説（知りたいこと）に応じて、以下の3つのケースについて計算式を示す。なお、これらの式において、zαはP(α)、z1-βは-zβ、Δは知りたい母平均との差（規格値と母平均との差/標準偏差）を表す。

母平均が指定値と異なることを示す場合（μ≠μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((zα/2 – z1-β)/Δ0)²

この場合の検出力の計算式は以下となる。
1-β = Pr(u≦-Zα/2-√nΔ) + Pr(u≧Zα/2-√nΔ)

母平均が指定値より大きいことを示す場合（μ＞μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((zα – z1-β)/Δ0)²

この場合の検出力の計算式は以下となる。
1-β = Pr(u≦Zα-√n*Δ)

母平均が指定値より小さいことを示す場合（μ＜μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((zα – z1-β)/Δ0)²

この場合の検出力の計算式は以下となる。
1-β = Pr(u≦-Zα-√n*Δ)

10.2 一つの母平均の検定におけるサンプルサイズの検討（母分散未知の場合）

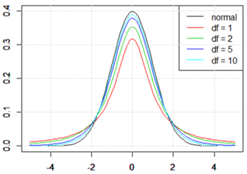
母分散が未知の場合においても、対立仮説に応じて3つのケースについて計算式を示す。この場合、母分散が未知であることを考慮した修正が必要となる。

母平均が指定値と異なることを示す場合（μ≠μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((Zα/2 – Z1-β)/Δ0)² + (Zα/2²/2)

この場合の検出力の計算式は以下となる。
w=-t(φ,α)とすると、
Pr(t₀>t(φ,α))=1-Pr(t₀<t(φ,α))
= 1 – Pr[u≦(w(1-1/(4φ))-λ)/√(1+w²/2φ)]

母平均が指定値より大きいことを示す場合（μ＞μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((Zα – Z1-β)/Δ0)² + (Zα²/2)

母平均が指定値より小さいことを示す場合（μ＜μ₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((Zα – Z1-β)/Δ0)² + (Zα²/2)

10.3 一つの母分散の検定におけるサンプルサイズの検討

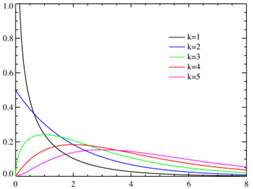
一つの母分散の検定におけるサンプルサイズの検討においては、対立仮説に応じて、以下の3つのケースについて計算式を示す。

母分散が指定値と異なることを示す場合（σ²≠σ²₀の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((Zα/2 – Δ01 Z1-β)/(3/2(Δ01-1)))² + 1（Δ01＞1の場合）
n ≒ ((Zα/2 – Δ02 Z1-β)/(3/2(Δ02-1)))² + 1（Δ02＜1の場合）

この場合の検出力の計算式は以下となる。
1-β = Pr{χ²≦χ²(n-1,1-α/2)/Δ²} + Pr{χ²≧χ²(n-1,α/2)/Δ²}

母分散が指定値より大きいことを示す場合（σ²/σ²₀＞1の場合）のサンプルサイズの近似式は以下となる。
n ≒ ((Zα – Δ0 Z1-β)/(3/2(Δ0-1)))² + 1

この場合の検出力の計算式は以下となる。
1-β = Pr{χ²≧χ²(n-1,α)/Δ²}

母分散が指定値より小さいことを示す場合（σ²/σ²₀＜1の場合）の計算式は σ²/σ²₀＞1 の場合と同じとなる。

10.4 母不良率の検定におけるサンプルサイズの検討

母不良率の検定におけるサンプルサイズの検討においては、対立仮説に応じた計算式を適切に選択する必要がある。これらの式を適用する際には、基本的な条件としてnP≧5およびn(1-P)≧5を満たす必要がある。また、全ての計算において、A = √(P0(1-P0)/(P(1-P)))およびB = (P-P0)/√(P(1-P)/n)という共通のパラメータを使用する。

母不良率が指定値と異なることを示す場合（P≠P₀の場合）には、検出力の式として以下を用いる。この場合、検出力の式に値を代入してnを計算する必要がある。
1-β ≒ Pr(u≦-Zα/2A-B) + Pr(u≧Zα/2A-B)

母不良率が指定値より大きいことを示す場合（P＞P₀の場合）には、以下の検出力の式を用いる。同様に、この式に値を代入してnを計算する。
1-β ≒ Pr(u≧ZαA-B)

母不良率が指定値より小さいことを示す場合（P＜P₀の場合）には、以下の検出力の式を用いる。
1-β ≒ Pr(u≦-ZαA-B)

これらの計算式は、母不良率の検定におけるサンプルサイズを決定する際の基本となるものである。実際の適用にあたっては、想定される母不良率の値や、要求される検出力に基づいて、適切なサンプルサイズを決定する必要がある。

10.5 二つの母平均の差の検定におけるサンプルサイズの決定

異なる二つの母集団の平均値を比較する場合について詳述する。各分散は未知であるが等しいと想定する。そのため、比較を行う前にあらかじめ分散の比の検定を実施する必要がある。

サンプルサイズの計算は以下の対立仮説に応じて行う必要がある。すべての場合において、σはあらかじめ予備実験等で想定しておく必要がある。

対立仮説「μ≠μ₀」（両側検定）の場合のサンプルサイズの計算式は以下となる。
n ≒ ((zα/2 – z1-β)/Δ0)² + zα/2²/4

対立仮説「μ＞μ₀」（片側検定）の場合のサンプルサイズの計算式は以下となる。
n ≒ ((zα – z1-β)/Δ0)² + zα²/4

対立仮説「μ＜μ₀」（片側検定）の場合のサンプルサイズの計算式は以下となる。
n ≒ ((zα – z1-β)/Δ0)² + zα²/4

検出力の計算式は、φ=n1+n2-2、λ=√(n1*n2/(n1+n2)) *Δとなる。ここでΔ=(μ1-μ2)/σであり、σはあらかじめ予備実験等で想定しておく必要がある。

1-β≒ Pr{t₀≦-t(n1+n2-2,α)} + Pr{t₀≧t(n1+n2-2,α)}

= Pr[u≦(-t(φ,α)(1-1/(4φ))-λ)/√(1+((-t(φ,α))²/2φ))] +
Pr[u≦(t(φ,α)(1-1/(4φ))-λ)/√(1+t(φ,α)²/2φ)]

なお、対立仮説「μ＞μ₀」の場合は以下となる。
1-β≒ Pr{t₀≧t(n1+n2-2,2α)}
= Pr[u≦(t(φ,2α)(1-1/(4φ))-λ)/√(1+t(φ,2α)²/2φ)]

対立仮説「μ＜μ₀」の場合は以下となる。
1-β≒ Pr{t₀≦-t(n1+n2-2,2α)}
= Pr[u≦(-t(φ,2α)(1-1/(4φ))-λ)/√(1+((-t(φ,2α))²/2φ))]

これらの式を用いて、目的に応じた適切なサンプルサイズを決定することができる。なお、実際の適用にあたっては、予備実験等により得られた分散の推定値を用いることが重要である。

10.6 二つの母不良率の差の検定

二つの母不良率の差の検定においては、対立仮説に応じた計算式を用いる。全ての場合において、nB = hnA（hは任意の数）という関係を前提とし、検出力の式に値を代入してnを計算する。また、計算の際には Pc = (nApA + nBpB)/(nA + nB) というパラメータを使用する。

二つの母不良率が異なることを示す場合（PA≠PBの場合）の検出力の計算式は以下の通りである。
1-β = 1-Pr[(-Δ+Zα/2√(Pc(1-Pc)(1/nA+1/nB)))/(√(PA(1-PA)/nA+PB(1-PB)/nB))] +
Pr[(-Δ-Zα/2√(Pc(1-Pc)(1/nA+1/nB)))/(√(PA(1-PA)/nA+PB(1-PB)/nB))]

第一の母不良率が第二の母不良率より大きいことを示す場合（PA＞PBの場合）の検出力の計算式は以下の通りである。
1-β = 1-Pr[(-Δ+Zα√(Pc(1-Pc)(1/nA+1/nB)))/(√(PA(1-PA)/nA+PB(1-PB)/nB))]

第一の母不良率が第二の母不良率より小さいことを示す場合（PA＜PBの場合）の検出力の計算式は以下の通りである。
1-β = Pr[(-Δ-Zα√(Pc(1-Pc)(1/nA+1/nB)))/(√(PA(1-PA)/nA+PB(1-PB)/nB))]

これらの検出力の計算式は、二つの母不良率の差を検定する際のサンプルサイズを決定するための基礎となる。特に、二つの群のサンプルサイズの比率を表すhの値は、研究デザインや実際の制約条件に応じて適切に設定する必要がある。検出力の計算結果に基づいて、必要なサンプルサイズを決定することができる。

10.7 二つの母分散の比の検定におけるサンプルサイズの検討

二つの母集団が同じ分散でないことが想定できる場合について、対立仮説に応じて計算式を示す。なお、これらの式においてΔ=σ1/σ2である。また、すべての計算式においてInは自然対数を表す。

二つの母分散が異なることを示す場合（σ1²≠σ2²の場合）のサンプルサイズの近似式は以下となる。
n ≒ 1 + ((zα/2 – z1-β)/InΔ1)²（Δ01＞1の場合）
n ≒ 1 + ((zα/2 – z1-β)/InΔ2)²（Δ02＜1の場合）

この場合の検出力の計算式は以下となる。
1-β = Pr{F₀≦F(φ1,φ2;α/2)/Δ²} + Pr{F₀≧F(φ1,φ2;α/2)*Δ²}

第一の母分散が第二の母分散より大きいことを示す場合（σ1²＞σ2²の場合）のサンプルサイズの近似式は以下となる。
n ≒ 1 + ((zα – z1-β)/InΔ0)²

この場合の検出力の計算式は以下となる。
1-β = Pr{F₀≧F(φ1,φ2;α)/Δ²}

第一の母分散が第二の母分散より小さいことを示す場合（σ1²＜σ2²の場合）のサンプルサイズの近似式は以下となる。
n ≒ 1 + ((zα – z1-β)/InΔ0)²

この場合の検出力の計算式は以下となる。
1-β = Pr{F₀≦1/(F(φ2,φ1;α))}

10.8 対応がある場合の母平均の差に関するサンプルサイズの検討

対応がある場合の母平均の差に関するサンプルサイズの検討は、一つの母平均の検定および区間推定と同じ考え方で行うことができる。この考え方は以下のような分布の関係に基づいている。

分布1のデータ（X11, X12, X13, X14, X15…）と分布2のデータ（X21, X22, X23, X24, X25…）から、それぞれの差（X11-x21, X12-x22, X13-x23, X14-x24, X15-x25…）を取ることで、差の分布を得ることができる。この差の分布は一つの母平均を持つ分布と考えることができるため、サンプルサイズの計算においても、一つの母平均の場合と同様の方法を適用することが可能である。

10.9 一つの母平均の区間推定に対するサンプルサイズの検討（母分散既知）

母分散が既知の場合の点推定、区間推定のためのサンプルサイズ計算、および区間推定について以下に示す。

点推定においては、以下の関係が成り立つ。
母平均 = サンプルの平均
σ₀ = 母標準偏差
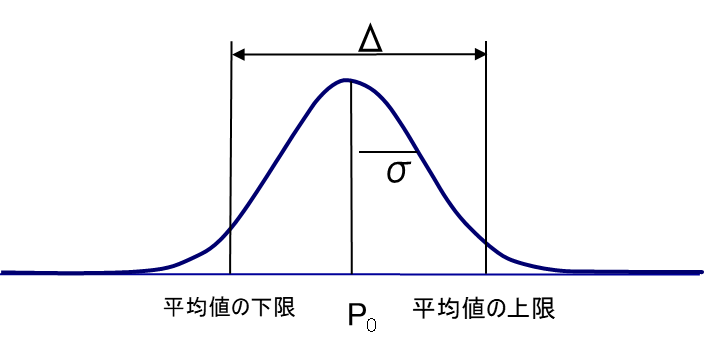
Δ = 信頼限界の上限から下限までの範囲

区間推定のためのサンプルサイズ計算は以下の式で行う。
n ≧ (4Zα/2²σ²)/Δ²

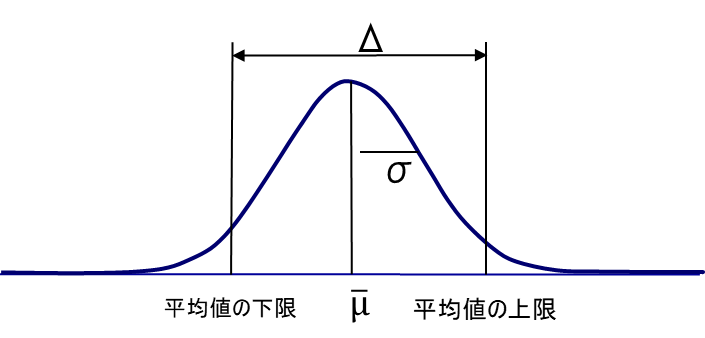
区間推定は以下の式で表される。
平均値の下限 = X̄ – Zα/2σ0/√n
平均値の上限 = X̄ + Zα/2σ0/√n

これらの式において、Zα = P(α)である。

10.10 一つの母平均の区間推定におけるサンプルサイズの検討（母分散未知）

母分散が未知の場合の点推定、区間推定のためのサンプルサイズ計算、および区間推定について以下に示す。

点推定においては、以下を用いる。
σ = あらかじめ計算したサンプルの標準偏差
Δ = 信頼限界の上限から下限までの範囲

区間推定のためのサンプルサイズ計算は以下の条件を満たすnを求める。
2t(n-1,α)(cσ)/√n ≦ Δ

ここで、cは以下の式で計算される。
c = √(2Γ(φ+1)/2)/(√φΓ(φ/2))

なお、Γ(m)はガンマ関数であり、m-1 * m-2 * … * 2 * 1で計算される。

区間推定は以下の式で表される。
平均値の下限 = X̄ – t(n-1,α)√V/√n 平均値の上限 = X̄ + t(n-1,α)√V/√n

10.11 一つの母分散の区間推定におけるサンプルサイズの検討

母分散の区間推定における点推定、区間推定のためのサンプルサイズ計算、および区間推定について以下に示す。

点推定においては、以下の式が成り立つ。
S/(n-1) = V = σ²

ここで、Sは分散の合計、Vは不偏分散（分散をn-1で割ったもの）を表す。

区間推定のためのサンプルサイズ計算は以下の式で行う。
n ≧ (1/2)(1 + Δ*Zα/2)²/(Δ-1)² + 3/2

区間推定は以下の式で表される。
下限 = (n-1)V/χ²(n-1,α/2)
上限 = (n-1)V/χ²(n-1,1-α/2)

ここで、Δは信頼上限/信頼下限を表す。

10.12 一つの母不良率の推定におけるサンプルサイズの決定

母不良率の推定における点推定、区間推定のためのサンプルサイズ計算、および区間推定について以下に示す。

点推定においては、以下の関係が成り立つ。
P0 = 母平均
P = サンプルの平均
σ₀ = √(P(1-P))
Δ = 信頼限界の上限から下限までの範囲

区間推定のためのサンプルサイズ計算は以下の式で行う。
n ≧ (4Zα/2²σ²)/Δ²

区間推定は以下の式で表される。
下限 = P – Zα/2√(σ0²/n)
上限 = P + Zα/2√(σ0²/n)

なお、これらの式においてnP≧5、n(1-P)≧5を満たす必要がある。

10.13 二つの母平均の差の区間推定におけるサンプルサイズの決定

二つの母平均の差の区間推定における点推定、区間推定のためのサンプルサイズ計算、および区間推定について以下に示す。

点推定においては、以下の関係が成り立つ。
μ1-μ2 = x̄1-x̄2

区間推定のためのサンプルサイズ計算は以下の近似式で行う。
n ≧ (8Zα/2²σ0²)/Δ²

ここで、Δは区間幅の期待値を表す。

n1 = n2 = nの場合の計算式は以下となる。
2t(2n-2,α)cσ/√(2n)がΔ条件を満たすnを求める。

ここで、cは以下の式で計算される。
c = √(2Γ(φ+1)/2)/(√φΓ(φ/2))

また、σはあらかじめ計算したサンプルの標準偏差であり、σ = σ₀とする。

区間推定は以下の式で表される。
下限 = X̄1 – X̄2 – t(n1+n2-2,α)√(V(1/n1 + 1/n2)) 上限 = X̄1 – X̄2 + t(n1+n2-2,α)√(V(1/n1 + 1/n2))

10.14 二つの母分散の比の区間推定におけるサンプルサイズの決定

二つの母分散の比の区間推定における点推定、区間推定のためのサンプルサイズ計算、および区間推定について説明する。

点推定においては、以下の関係が成り立つ。
σ1/σ2 = V1/V2 = s1/(n1-1)/(s2/(n2-1))

ここで、Sは分散の合計、Vは不偏分散（分散をn-1で割ったもの）を表す。Δは信頼上限/信頼下限を表す。信頼率を1-αとし、n1 = n2 = nの場合について考える。

サンプルサイズ計算は、以下の条件を満たすnを求めることで行う。
{F(n-1,n-1,α/2)}² ≦ Δ

区間推定は、分散を直接計算して求める必要がある。計算された分散から、母分散の比の信頼区間を構築することができる。これにより、二つの母集団の分散の違いについて統計的な推定を行うことが可能となる。

二つの母分散の比の区間推定においては、F分布を用いた信頼区間の構築が重要となる。この手法は、二つの母集団の分散の比較において、特に製造工程や品質管理の分野で広く活用されている。例えば、二つの製造ラインの安定性を比較する場合や、測定機器の精度を評価する場合などに適用することができる。

なお、この計算方法を適用する際の前提条件として、二つの母集団が正規分布に従っていることと、サンプルが互いに独立であることが求められる。これらの条件が満たされない場合は、別の統計的手法を検討する必要がある。

また、サンプルサイズの決定においては、目的とする信頼水準と許容される区間幅を考慮しながら、実用的な観点からも適切なサイズを選択することが重要である。特に、コストや時間的な制約がある場合は、これらの要因も考慮に入れながら、統計的に意味のある結果が得られるサンプルサイズを決定する必要がある。